Гидродинамика

Гидродинамика изучает движение жидкости, которое может быть установившимся и не установившимся.

Движение называется установившимся, если в каждой точке неподвижного пространства, занятого движущейся жидкостью, ско-

 

 

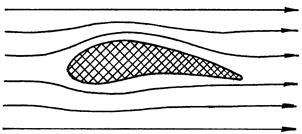
рости не зависят от времени и, следовательно, остаются постоянными. В противном случае движение является неустановившимся.

Характер движения жидкости может быть ламинарным и турбулентным. Под ламинарным движением жидкости понимают такое движение, в котором отсутствует пульсация скоростей, приводящая к перемешиванию частиц. Если движение жидкости происходит с пульсацией скоростей, вызывающей перемешивание частиц потока, то такое движение называется турбулентным.

В гидродинамике используется понятие о линиях тока. Линии тока - линии, касающиеся вектора скорости потока. При установившемся движении жидкости линии тока и траектории движения частиц жидкости совпадают, при неустановившемся - не совпадают.

Поверхность, образуемую линиями тока, проходящими через замкнутый контур, называют трубкой тока; жидкость, заполнившая трубку тока, - элементарной струйкой.

Наглядное представление о линиях тока дает рассмотрение обтекания крыла самолета равномерным потоком воздуха. Из рис.3. видно, что снизу линии тока не очень сильно искажены, т.к. там увеличение скорости потока незначительно. Верхняя сторона крыла гораздо сильнее изменяет течение воздуха - там линии тока сжимаются и скорость заметно больше, чем в самом потоке.

 

Рис.3. Обтекания крыла равномерным Рис.4. К выводу уравнения

потоком воздуха. Бернулли.

 

Описать движение жидкости гораздо труднее, чем решить задачи гидростатики, поэтому в гидродинамике широко используют уравнения неразрывности и уравнения Бернулли.

 

 

Уравнение неразрывности выражает закон сохранения масс и используется в форме:

υ₁S₁ = υ₂S₂ = …= υ_nS_n = Q = const.

 

Здесь υ-скорость жидкости, S - площадь сечения трубки тока, Q - объемный расход потока. Сформулировать этот закон можно так: через любое поперечное сечение трубки тока в единицу времени протекает одинаковое количество жидкости.

Одно из важнейших уравнений гидромеханики было получено Даниилом Бернулли (рис.4.). Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:

р + ρυ²/2 + ρgh = const,

где р - давление жидкости, ρ - ее плотность, υ - скорость движения, g - ускорение свободного падения и h - высота, на которой находится элемент жидкости. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости.

В этом уравнении все слагаемые имеют размерность давления и соответственно называются:

р - статическое давление;

ρυ²/2 - динамическое давление;

ρgh - весовое давление.

Можно отметить, что при отсутствии скорости уравнение Бернулли превращается в гидростатическую формулу. Изменение скорости, согласно второму закону Ньютона, происходит под действием силы, которая действует на жидкость, - в данном случае это либо сила тяжести, либо разность давлений, действующих на объем текущей жидкости.

В уравнении Бернулли два слагаемых:

ρυ²/2 - кинетическая энергия единицы объема движущейся жидкости и ρgh - потенциальная энергия единицы объема жидкости,

точно такие, как в уравнении сохранения энергии для материальной точки. Специфика гидромеханики проявляется в присутствии давления р - перепад давлений в разных частях трубки тока заставляет жидкость двигаться с ускорением, и именно поэтому в формуле Бернулли помимо кинетической и потенциальной энергий единицы объема жидкости присутствует еще и давление.

 

Следовательно, если труба (или трубка тока) устроена так, что давление в ней остается постоянным, уравнение Бернулли для жидкости просто совпадает с законом сохранения энергии для материальной точки. Если же труба устроена так, что можно не учитывать изменение высоты h (в силу малой плотности вещества или малого изменения этой высоты), то в соответствии с уравнением неразрывности скорость в узких участках трубы растет, - значит, там должно падать давление. Это естественный результат, поскольку рост скорости (ускорения) может быть обеспечен только за счет перепада давления и в том месте, где скорость большая, давление должно быть мало.

Уравнение Бернулли просто объясняет множество явлений рассматриваемых в курсе “теория судна”. Например, крыло, которое обтекает равномерный поток воды даже при отсутствии угла атаки, имеет подъемную силу. На суда идущими параллельным курсом слишком близко один к другому, действует гидродинамическая сила, толкающая их друг к другу. Большие скорости потока жидкости, создающиеся при быстром вращении судового винта, приводят к появлению кавитации, способной разрушить его лопасти. Принцип работы судового лага, основан также на уравнении Бернулли, позволяющий измерить скорость движения жидкости.