Влияние приема малого груза на посадку и остойчивость судна
Изменение посадки судна при приеме груза рассматривалось в § 4.4. Определим изменение поперечной метацентрической высоты δh при приеме малого груза массой m (рис.49), центр тяжести которого располагается на одной вертикали с ЦТ площади ватерлинии в точке с аппликатой z.
В результате увеличения осадки объемное водоизмещение судна увеличится на δV = m /ρ и возникнет дополнительная сила плавучести γ δV, приложенная в ЦТ слоя между ватерлиниями WL и W1L1.
Рис.49. Прием на судно малого груза
Считая судно прямобортным, аппликата ЦТ дополнительного объема плавучести будет равна d + δd /2, где приращение осадки определим по известным формулам δd = m/ ρS или δd = m / qсм. При наклонении судна на угол Θ, сила веса груза р и равная ей сила плавучести γ δV составляют пару сил с плечом (d + δd /2 –z)sinΘ. Момент этой пары δmΘ = р (d + δd /2 – z) sin Θ увеличивает первоначальный восстанавливающий момент судна mΘ = γV h sin Θ, поэтому восстанавливающий момент после приема груза становится равным mΘ1 = mΘ + δmΘ, или (γV + γ δV)(h + δh) sin Θ = γV h sin Θ + γ δV(d + δd /2 – z) sin Θ, перейдя к массовым значениям, получим (Δ + m)(h + δh) sin Θ = Δ h sin Θ + m (d + δd /2 – z) sin Θ. Из уравнения найдем приращение метацентрической высоты δh:
Для общего случая приема или снятия малого груза формула примет вид:
где + (–)подставляется при приеме (снятии)груза. Из формулы видно, что δh < 0 при z > (d ± δd /2 – h) и δh > 0 при z < (d ± δd /2 – h), а δh = 0 при z = (d ± δd /2 – h). Уравнение z = (d ± δd /2 – h) является уравнением нейтральной (предельной) плоскости. Нейтральная плоскость, является плоскостью, прием на которую груза не изменяет остойчивость судна. Прием груза выше нейтральной плоскости уменьшает остойчивость судна, ниже нейтральной плоскости увеличивает ее.
|


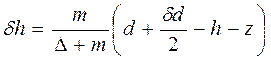
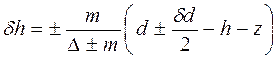 или:
или: ,
,


