Винт жұптарының теориясы.
Жоғарыда баяндалғандай, бұранда сызығын жазсақ көлбеу жазықтық пайда болады, ал гайканы жазықтықта сырғитын дене ретінде қарауға болады (13.5-сурет). Суреттегі Fa — винтке ось бойымен әсер ететін күш; a - бұранданың көтерілу бұрышы; j — үйкеліс бұрышы; Сонда гайкаға екі күш: гайканы бұрау күші және гайка тартылғанда пайда болатын осьтік күші әсер етеді. Гайканы біp айналдырып бұрағанда, гайка көлбеу жазыктықпен жылжып, біp аралыққа көтеріледі. Осыған орай, механика заңы бойынша (үйкеліcті есептемесек) істелген жұмыс пен пайдалы жұмыс біp-біpiнe тең болады:
мұндағы dop — бұранданың орташа диаметрі; Рh — бұранда жүpici; біp кірмелі бұрандалар үшін Рh = P. P1 =P=pdop tg a, P — бұранда қадамы.
Ft = Fa tg a (13.2) Бұранданы бұрағанда екі түрлі кедергі кездеседі: бұранданың өзінде кездесетін кедергі және гайканың табанында пайда болатын кедергі. Олай болса, тарту моменті бұранда мен табанындағы моменттердің қосындысына тең болады
Бұрандадағы момент үйкеліс күшін есептегенде былай табылады:
мұндағы j - үйкеліс бұрышы. Үйкеліс бұрышы үйкеліс коэффициенті арқылы табылады j = arctg f, f— бұрандадағы үйкеліс коэффициенті. Гайка табанындағы үйкеліс моменті. Гайканың және оның қалпақшасының жанасу бетін шамамен шеңбер ретінде қарауға болады. Сонда кілт қамтитын диаметрді шеңбер бетінің сыртқы диаметріне тең деп, ал винт енетін тесіктің диаметрін ішкі диаметрге тең деп қарауға болады. Егер Fa күші тіpeк бетіне бірқалыпты тарайды деп есептесек, онда
D1—кілттің диаметрі; dT — винт кіpeтін тecіктің диаметрі; q — меншікті қысым. Сонда гайка табанындағы момент былай анықталады:
Ал үйкеліс моменті
Орташа диаметрді техникалық есептеуде былай да алуға болады:
Егер орташа есеппен алғанда d2 = 0,9d, d'op = l,2d, T = 0,2Fa d және кілттің ұзындығы 14d болса, онда біз көрсетілген формула бойынша күштен 70...100 есе ұтамыз. Сондықтан бұранда қосылысы техникада көп қолданылады. Бұрандалардың пайдалы әсер коэффициенті. Пайдалы әсер коэффициенті деп винттегі пайдалы жұмыстың (Fa p) істелген (Ft pdop) жұмысқа қатынасын айтады:
Егер винттің табанындағы үйкелісті есепке алсақ
ал кepі бұраған кезде
Гайканы немесе винттің қалпақшасын кepі бұрауға қажетті момент бұранда моментіне шамалас, тек қана момент пен үйкеліc күшінің бағыты кері өзгереді. Онда өздігінен тежелу шарты мынаған тең болады:
Егер бұранда үшін гайканың табанындағы үйкелісті есепке алмасақ: Егер a<j болса, онда бұранда өздігінен тежеу қасиетіне ие болады, гайканы қосымша бекітудің қажеті жоқ. Бекітуші бұрандалар үшін көтерілу бұрышы — a =1,5...40-қа дейін; ал үйкеліc бұрышы — j=60...160-ºа дейін өзгереді. Көрсетілген (8.7) формуласы бойынша a бұрышын үлкейтетін болсақ, жоғарылайды. Біpaқ бұрандалар өздігінен тежелу қасиетінен айырылады. Сондықтан, бекіту бұрандаларында a бұрышы j бұрышынан аз болуы қажет a<j. Ал жүкті көтеретін, қозғалыс беретін бұрандаларда, пайдалы әсер коэффициенті жоғары болуы керек. Бірақ көтерілу бұрышы a = 20...250-тан асқанда бұрандаларды дайындау қиынға түседі. Сондықтан a = 180...250 аралығында болуы қажет. Пайдалы әсер коэффициентін көбейту үшін винтті механизмдерде түрлі амалдар, мысалы, үйкеліс коэффициенті аз металдарды үйкеліс беттepін мұқият өңдеу және майлау, шарикті винт жұбы және т. б. қолданылады.
13.5-сурет. Гайканың тарту анықтау 13.6- сурет. Винт пен гайка арасындағы әсер ететін күштер схемасы
Негізгі әдебиеттер: 2[59-82;86-91] Қосымша әдебиеттер: 20[27-45;70-85] Бақылау сұрақтар: 1. Қосылыстардың классификациясы, түрі, қойлатын талаптары. 2. Винтік жұптың өздігінентепселенуі әр кезде керек пе? 3. Кілтектіқ қосылыстарының түрлері, қолдануы.
|

 , (13.1)
, (13.1)

 (13.3)
(13.3) (13.4)
(13.4)
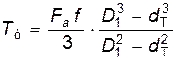 . (13.5)
. (13.5) . Егер осы формуламен есептесек, винт басынын немесе гайканың табанындағы момент барлық жұмсалған моменттің жартысына тең болады. Ал барлық тартылу моменті:
. Егер осы формуламен есептесек, винт басынын немесе гайканың табанындағы момент барлық жұмсалған моменттің жартысына тең болады. Ал барлық тартылу моменті: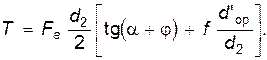 (13.6)
(13.6) (13.7)
(13.7) , (13.8)
, (13.8)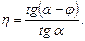 (13.9)
(13.9) TT ³ 0 (13.10)
TT ³ 0 (13.10)




