Экспериментальное определение составляющих полного перемещения
Здесь n - число ступеней нагружения. 6. По окончании эксперимента балку разгрузить и сравнить показания индикаторов после разгрузки с первоначальными. 7. Вычислить приращения нагрузки Δ Fi, приращения показаний индикаторов Δ f верт. i, Δ f гор. i для каждой i - ой ступени нагружения; средние арифметические значения приращений
8. Вычислить экспериментальное значение угла γ; (см. рис. 6.1) по формуле: 9. Вычислить величины теоретического полного перемещения 10. Определить расхождение между теоретическими и экспериментальными значениями полного перемещения и угла γ;:
Вопросы для самопроверки 1. Что называется косым изгибом? 2. Напишите формулу для определения положения нулевой линии. Объясните физический смысл всех величин, входящих в формулу. 3. Определите положение нулевой линии при плоском косом изгибе балки прямоугольного поперечного сечения, если силовая линия совпадает с диагональю поперечного сечения. 4. Какое положение занимает плоскость изгиба балки квадратного поперечного сечения, если силовая линия совпадает с диагональю поперечного сечения? 5. Напишите условие, при котором деформация косого изгиба невозможна, объясните почему? 6. Дайте определение плоского и пространственного косого изгиба? 7. При косом изгибе плоскость изгиба отклоняется от плоскости действия сил. В какую сторону она отклоняется? В сторону главной плоскости наибольшей или наименьшей жесткости? Объясните это, пользуясь соответствующей формулой. 8. При какой форме поперечного сечения балки косой изгиб невозможен и почему? 9. Для исследуемой в лабораторной работе балки вычислите отношение составляющих перемещения fz/fy при α; = 450.
|



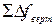




 ,
, 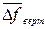 ,
,  , а также среднее приращение полного перемещения:
, а также среднее приращение полного перемещения: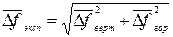 .
. .
. и угла
и угла  по формулам (6.2 – 6.4), принимая
по формулам (6.2 – 6.4), принимая  ,
,  ,
,  .
. ;
;  .
.


