Теоретическая часть. Изгибназывают косым,если плоскость действия изгибающего момента, возникающего в поперечном сечении балки
Изгиб называют косым,если плоскость действия изгибающего момента, возникающего в поперечном сечении балки, не совпадает ни с одной из его главных плоскостей. Главные плоскости ХОУ и ХОZ проходят через продольную ось балки ОХ и главные центральные оси поперечного сечения 0У, 0Z. Различают плоский косой изгиб и пространственный косой изгиб. При плоском косом изгибе все нагрузки расположены в одной плоскости, т.е. существует общая для всей балки силовая плоскость. В этом случае упругая линия балки - плоская кривая, но в отличие от прямого изгиба, плоскость, в которой она расположена, не совпадает с силовой плоскостью. Именно эта особенность характера деформации обуславливает наименование косой изгиб. При пространственном косом изгибе нагрузки, вызывающие изгиб, расположены в разных продольных плоскостях балки. Соответственно углы между главными центральными осями поперечных сечений и силовыми линиями не постоянны по длине балки. Упругая линия балки в этом случае - пространственная кривая. Косой изгиб можно рассматривать как совокупность двух прямых изгибов во взаимно перпендикулярных главных плоскостях балки. Перемещения при косом изгибе определяют на основе принципа независимости действия сил путем геометрического суммирования перемещений, получающихся в направлении главных осей. Полное перемещение будет равно:
Нулевой, или нейтральной линией, называется геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю. Нормальные напряжения в произвольной точке поперечного сечения определяются на основе принципа независимостидействия сил, как алгебраическаясумма нормальных напряжений
Для получения уравнений нулевой линии приравниваем нулю правую часть выражения:
Эта формула показывает, что нулевая линия – прямая, проходящая через начало координат и составляющая с осью z угол, определяемый из выражения:
Обозначим α - угол наклона силовой линии к оси 0У (рис. 6.1), тогда
Анализируя последнее выражение, приходим к выводу, что в отличие от прямого изгиба нулевая и силовая линии не будут взаимно перпендикулярны. Здесь угол β; отсчитывается от оси z, а угол α; - от оси y, и условие перпендикулярности силовой и нулевой линии будет tgβ; = - tgα; (см. рис. 6.1). Лишь в частном случае, когда Iz = Iy, угол между нулевой и силовой линиями будет прямым (tgβ; = - tgα;), но это значит, что любая центральная ось сечения – главная ось, а значит, вообще изгиб будет прямым. Для сечений типа круга, квадрата и т. п., у которых все центральные оси – главные (Iz = Iy), косой изгиб невозможен. Нулевая и силовая линии проходят через разные квадранты сечения: так, например, если силовая линия проходит через I и III квадранты, то нулевая линия – через II и IV. Угол между силовой линией и направлением полного перемещения (следом плоскости изгиба) обозначим γ; (см. рис. 6.1), он равен: γ= β; - α;. (6.3) Величина угла γ; тем больше, чем больше отношение Iz/Iy.
Универсальное уравнение упругой линии балки в данном случае будет иметь вид:
где Тогда прогиб на свободном конце консоли при
Если сила F будет направлена под некоторым углом α; к оси 0Y (рис. 6.2, б), то для определения полного перемещения f по формуле (6.1) предварительно необходимо вычислить перемещения fy, fz в главных плоскостях балки:
Учитывая, что
|

 . (6.1)
. (6.1) и
и  , каждое из которых обусловлено одним из прямых изгибов:
, каждое из которых обусловлено одним из прямых изгибов: .
. или
или  .
.
 .
.
 и
и (6.2)
(6.2) Для теоретического определения прогибов балки можно использовать любой из изученных методов. Определим прогиб свободного конца консоли, загруженной сосредоточенной силой (рис. 6.2, а), используя метод начальных параметров.
Для теоретического определения прогибов балки можно использовать любой из изученных методов. Определим прогиб свободного конца консоли, загруженной сосредоточенной силой (рис. 6.2, а), используя метод начальных параметров. ,
, ;
;  - реакция и момент в заделке. Прогиб
- реакция и момент в заделке. Прогиб  и угол поворота сечения
и угол поворота сечения  в заделке будут равны нулю.
в заделке будут равны нулю.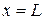 (стрела прогиба):
(стрела прогиба):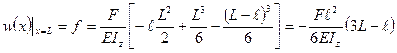
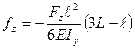 ;
;  .
. ;
;  , получим расчетную формулу для вычисления теоретического полного перемещения в следующем виде:
, получим расчетную формулу для вычисления теоретического полного перемещения в следующем виде: . (6.4)
. (6.4)


