Теоретическая часть. Внецентренное растяжение-сжатие – это частный случай сложного сопротивления, когда на брус действует сосредоточенная сила
Внецентренное растяжение-сжатие – это частный случай сложного сопротивления, когда на брус действует сосредоточенная сила, параллельная оси бруса, приложенная не в центре тяжести поперечного сечения (рис. 7.1).
Величины ВСФ во всех сечениях будут одинаковы. Напряжения в произвольной точке определяются алгебраической суммой:
Нейтральная или нулевая линия – геометрическое место точек поперечного сечения, в которых σ; = 0. Приравниваем выражение σ; к нулю и после преобразований получим уравнение нулевой линии (рис. 7.2):
где
Ядром сечения называется действительная или мнимая часть поперечного сечения, расположенная вокруг его центра тяжести, обладающая тем свойством, что приложение растягивающей или сжимающей силы в ней вызывает появление во всем поперечном сечении напряжения только одного знака. В тех случаях, когда н. л. касается контура поперечного сечения, нигде его не пересекая, точка приложения внецентренной нагрузки будет расположена на контуре ядра сечения. Умение строить ядро сечения очень важно при проектировании сооружений из хрупких материалов, т.к. такие материалы плохо работают на растяжение и для них не желательно, чтобы растягивающие напряжения возникали хотя бы в некоторой части поперечного сечения. Для построения ядра сечения нужно провести последовательно несколько н. л., касающихся точек контура поперечного сечения, нигде не пересекая его, как это выполнено на рис. 7.3. Так как при этом точка приложения силы F будет располагаться на контуре ядра сечения, то обозначим ее координаты zя, yя.
Распределение нормальных напряжений по поперечному сечению зависит от расположения точки приложения внецентренной нагрузки по отношению к ядру сечения. С целью упрощения анализа, рассмотрим характерные случаи приложения сжимающей силы F в точках, расположенных на одной из главных центральных осей инерции поперечного сечения (yF = 0), т.е. случай внецентренной нагрузки, приводящей к одновременному действию осевого усилия и чистого плоского изгиба. Четыре характерных случая показаны на рис. 7.4 с согласованием между собой точки приложения силы относительно ядра сечения с видом эпюры напряжений. В первом случае нагрузка приложена в центре тяжести поперечного сечения и напряжения равномерно распределены по поперечному сечению, а нулевая линия расположена в бесконечности. Во втором случае – сила приложена в области ядра сечения и нулевая линия не пересекает контур поперечного сечения, а напряжения во всех точках сечения имеют одинаковый знак.
В третьем случае точка приложения силы лежит на контуре ядра сечения и нулевая линия касается контура поперечного сечения. В четвертом случае – сила приложена за пределами ядра сечения и нулевая линия пересекает контур поперечного сечения, разделяя сечения на зоны растяжения и сжатия.
В качестве образца используется стальной призматический брус, Размеры поперечного сечения которого, места наклейки тензодатчиков и координаты приложения сжимающей силы показаны на рис. 7.5. Нагрузка на образец прикладывается шариком пресса ТШ-2. Измерение деформаций проводится с помощью прибора ИДЦ-1.
|

 В сечениях бруса возникает 3 внутренних силовых факторов (ВСФ) N = - F; My = FzF; Mz = Fzy.
В сечениях бруса возникает 3 внутренних силовых факторов (ВСФ) N = - F; My = FzF; Mz = Fzy.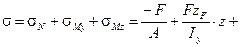
 .(7.1)
.(7.1) , (7.2)
, (7.2) ;
; 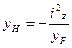 - отрезки, отсекаемые нулевой линией на осях координат; iy, iz - радиусы инерции поперечного сечения.
- отрезки, отсекаемые нулевой линией на осях координат; iy, iz - радиусы инерции поперечного сечения. Если нулевая линия (н. л.) пересекает контур поперечного сечения, то в сечении можно выделить две области, лежащие по разные стороны от нулевой линии и имеющие различные знаки напряжений. Одна область поперечного сечения будет растянутой и напряжения в ней будут положительными, а другая – сжатая.
Если нулевая линия (н. л.) пересекает контур поперечного сечения, то в сечении можно выделить две области, лежащие по разные стороны от нулевой линии и имеющие различные знаки напряжений. Одна область поперечного сечения будет растянутой и напряжения в ней будут положительными, а другая – сжатая. Эти координаты точек, соответствующие определенным положениям н.л., находятся из выражения (7.2), если решить их относительно zF = zя, yF = yя, а именно:
Эти координаты точек, соответствующие определенным положениям н.л., находятся из выражения (7.2), если решить их относительно zF = zя, yF = yя, а именно: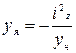 ,
,  (7.3)
(7.3)



 Оборудование и образцы
Оборудование и образцы


