Экспериментальная часть. Обработка результатов. Для аналитического определения перемещений в произвольной упругой системе рекомендуется следующий порядок.
1. Нарисовать действительную (грузовую) систему и загрузить ее всеми внешними нагрузками (рис. 8.3, а). Нарисовать фиктивную (единичную) систему, имеющую такие же размеры, форму и способы закрепления, как и действительная. Нагрузить фиктивную систему единичной силой,соответствующей искомому перемещению (пример нагружение для определения горизонтального перемещения показан на рис. 8.3, б). 3. Определить внутренние усилия на всех участках единичной системы; результат занести в табл. 8.2. 4. Значения внутренних усилий подставить в интеграл Максвелла-Мора и вычислить его. При выполнении третьего и четвертого пунктов, необходимо учитывать, что ось х - продольная на всех участках. Момент относительно оси х является крутящим; относительно осей у и z - изгибающим. Знаменатели в интеграле Максвелла-Мора соответствуютразновидностям внутреннихусилий и являютсяжесткостью при изгибе и кручении относительно соответствующих осей. Определяем внутренние усилия,размещая начало текущей системы координат в центре тяжести произвольногосечения каждого участка, двигаясь, каждый раз от свободного конца бруса в сторону защемления. В качестве примера покажем, как определять внутренние усилия на первых трех участках ломаного бруса. Первый участок (рис. 8.4, а). В грузовой системе в пределах участка внешних нагрузок нет. Следовательно, и внутренние усилия равны нулю. В единичной системе внешняя сила, равная 1, пересекает ось х и параллельна оси z, следовательно, Второй участок (рис. 8.4, б). В грузовой системе Mx = Т = 0, т. к. сила F пересекает ось х; My = 0 поскольку ось у и сила F параллельны. Изгибающий момент относительно оси z: Mz=-Fx2. В единичной системе
Третий участок (рис. 8.4, в). В грузовой системе отличными от нуля являются крутящий момент Mx = Т = F(e - a) и изгибающий момент в вертикальной плоскости Mz=-Fx3. В единичной системе только один момент отличен от нуля - в горизонтальной плоскости 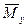 = 1·a. Эпюры моментов для этих участков показаны на рис. 8.5. = 1·a. Эпюры моментов для этих участков показаны на рис. 8.5.
Замечание о знаках. Знаки моментов устанавливаются в соответствии с правилами, принятыми в сопротивлении материалов, однако для решения поставленной задачи не имеет значение, какое именно правило принято. Важно, чтобы оно для грузовой и единичной систем было единым хотя бы в пределах участка, поскольку под интегралом Максвелла-Мора стоит произведение моментов. Для удобства вычислений интеграла Максвелла-Мора полезно воспользоваться связью между геометрическими характеристиками Ip = 2 Iz и упругими постоянными (принимая для стали μ; = 0,3)
Тогда получим GIp = 0,8 EIz.
|

 Для аналитического определения перемещений в произвольной упругой системе рекомендуется следующий порядок.
Для аналитического определения перемещений в произвольной упругой системе рекомендуется следующий порядок.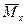 =
= 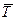 = 0;
= 0; 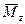 = 0. Отличным от нуля является лишь
= 0. Отличным от нуля является лишь 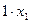 .
.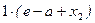 .
.
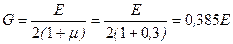 .
. Таблица 8.2
Таблица 8.2


