Теоретическая часть. Для системы, n раз статически неопределимой, канонические уравнения метода сил записываются в виде:
Для системы, n раз статически неопределимой, канонические уравнения метода сил записываются в виде:
где Каждое i -ое уравнение устанавливает равенство нулю перемещения в направлении i -ого лишнего неизвестного Хi от действия на основную систему внешней нагрузки и всех лишних неизвестных. Коэффициенты Свободные члены Все перемещения определяются методом Мора. Число лишних неизвестных равно степени статической неопределимости системы i. Степень статической неопределимости для плоских рам и балок определяется формулой: i = n – 3, где n – число реакций опор.
Для системы один раз статически неопределимой уравнения (9.1) принимают более простой вид:
откуда находим: От выбора лишней неизвестной зависит вид основной системы. Для расчетной схемы (рис. 9.1, а) примем за лишнюю неизвестную реакцию опоры X 1 = YB. Основная и эквивалентная системы при таком выборе лишней неизвестной показаны на рис. 9.1, б, в. Для вычисления перемещений Тогда по методу Мора перемещения будут равны:
где
Теоретическое значение момента в заделке
На используемой лабораторной установке экспериментально определяется непосредственно момент в заделке МА, поэтому целесообразно в качестве лишней неизвестной выбрать момент в заделке X 1 = MA. В этом случае основная и эквивалентная системы будут другими, но теоретическое значение момента MAтеор будет получено сразу из канонического уравнения метода сил. Суть работы заключается в сравнении теоретического MAтеор и момента определённого экспериментально на установке.
|

 (9.1)
(9.1)
 — лишние неизвестные:
— лишние неизвестные:  ,
, 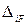 —коэффициенты и свободные члены канонических уравнений метода сил.
—коэффициенты и свободные члены канонических уравнений метода сил. называют единичными перемещениями – это перемещения в основной системе, вызванные j -й единичной неизвестной
называют единичными перемещениями – это перемещения в основной системе, вызванные j -й единичной неизвестной  , точки приложения i -й лишней неизвестной в направлении её действия.
, точки приложения i -й лишней неизвестной в направлении её действия. На рис. 9.1, а показана один раз статически неопределимая балка. Для неё число реакций опор n = 4 (МА, YA, XA, YB) и i = 4 – 3 = 1.
На рис. 9.1, а показана один раз статически неопределимая балка. Для неё число реакций опор n = 4 (МА, YA, XA, YB) и i = 4 – 3 = 1. (9.2)
(9.2) . (9.3)
. (9.3) и
и  необходимо рассмотреть основную систему в двух состояниях: единичном, нагруженном только единичной силой (рис. 9.1, г) и грузовом, нагруженном только внешними силами (рис. 9.1, д).
необходимо рассмотреть основную систему в двух состояниях: единичном, нагруженном только единичной силой (рис. 9.1, г) и грузовом, нагруженном только внешними силами (рис. 9.1, д).
 ,
, - изгибающий момент на i -том участке от действия единичной силы
- изгибающий момент на i -том участке от действия единичной силы  на основную систему (единичное состояние см. рис. 9.1, г);
на основную систему (единичное состояние см. рис. 9.1, г);  - изгибающий момент от действия внешней нагрузки на основную систему (грузовое состояние см. рис. 9.1, д).
- изгибающий момент от действия внешней нагрузки на основную систему (грузовое состояние см. рис. 9.1, д). .
. определяется из уравнения равновесия для эквивалентной системы (см. рис. 9.1, в):
определяется из уравнения равновесия для эквивалентной системы (см. рис. 9.1, в): :
:  .
.


