Формула Эйлера для критической силы
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F (рис. 10.4). Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M: M = −Fy, где y – прогиб стержня в произвольном сечении с координатой x. При шарнирном опирании концов стержня продольный изгиб произойдёт в плоскости наименьшей жёсткости, т. е. поперечные сечения будут поворачиваться вокруг оси, относительно которой момент инерции имеет минимальное значение Imin. В этом легко убедиться, сжимая гибкую линейку. Предположим, что деформации малые и напряжения в стержне не превышают предела пропорциональности σ;пц. Тогда для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии: EIminу"= Mизг, где у" = d 2 y / dx 2. Учитывая противоположные знаки для изгибающего момента и прогиба, имеем: EIminу" = -Fy. (10.1) В самом деле, если стержень изогнут, как показано на рис. 10.4, то М >; 0, а у <; 0, если стержень изогнут в другую сторону, то знаки меняются на противоположные. Введя обозначение: F/(EImin) = k2, (10.2) перепишем формулу (10.1): у"; + k2 у = 0. Общее решение полученного однородного дифференциального уравнения представляется функцией y = C 1 sin kx +C 2 cos kx. (10.3) Это решение содержит три неизвестные: постоянные интегрирования С 1 и С 2 и параметр k. Найдем эти величины из граничных условий – условий закрепления стержня по концам: а) при x = 0 прогиб в опоре (точка A) должен быть равен нулю y = 0, тогда из уравнения (10.3) получим, что С 2 = 0, при этом формула приобретает вид: y = C 1 sinkx. (10.4) Уравнение (10.4) указывает на то, что при продольном изгибе изогнутая ось стержня может быть представлена как некоторое число волн синусоиды с амплитудой C 1. б) при x = l прогиб в другой опоре (точка B) должен быть также равен нулю y = 0, тогда из уравнения (4) получим, что C 1 sin kl = 0.Согласно постановке задачи, коэффициент C 1 заведомо не равен нулю (иначе равен нулю прогиб балки во всех точках, что противоречит постановке задачи). В этом случае получаем sinkl = 0. Из свойств синусоиды следует, что k = n π/l, (10.5) где n – произвольное целое число, которое представляет собой число полуволн синусоиды, укладывающихся на длине изогнутой оси стержня (n ≠ 0, если n = 0, то k = 0 и F = 0, в соответствии с (10.2)). Решая совместно уравнения (10.2) и (10.5),получим выражение для некоторых фиксированных значений сжимающей силы, при которых возможна криволинейная форма равновесия оси стержня F= n 2 π;2 EImin /(l 2). Как видим, минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) F= π;2 EImin /(l 2). (10.6) Это выражение обычно называют ф о р м у л о й Э й л е р а, а определяемую с ее помощью критическую силу – э й л е р о в о й с и л о й. Критической силе, определяемой по формуле (10.6), соответствует изгиб стержня по синусоиде с одной полуволной: y = sin (πz/l). Следует отметить, что постоянная C 1, а, следовательно, и форма изогнутой оси стержня остались неопределёнными. Если применить для исследования продольного изгиба не приближённое, а точное дифференциальное уравнение изогнутой оси, то оказывается возможным определить не только величину критической силы, но и зависимость между сжимающей силой и прогибом стержня.
|

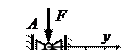 Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.


