Пределы применимости формулы Эйлера. Формула Ясинского
Формулой Эйлера не всегда можно пользоваться. При её выводе использовалось приближённое дифференциальное уравнение изогнутой оси балки, вывод которого основан на законе Гука. Закон же Гука справедлив до тех пор, пока напряжения не превосходят предела пропорциональности. Для того чтобы установить пределы применимости формулы Эйлера, определим критическое напряжение, т. е. напряжение, возникающее в поперечном сечении стержня при действии критической нагрузки:
где Формула Эйлера получена при предположении, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности
Записываем эту формулу относительно гибкости и находим, что
Величину, стоящую в правой части этого неравенства, обозначим
В отличие от гибкости стержня, представляющей собой его геометрическую характеристику, предельная гибкость зависит только от физико-механических свойств материала и не зависит от его размеров. Предельная гибкость – постоянная для данного материала величина. Например, для стали Ст3 при σпц = 200 МПа, Е = 2·105 МПа получим Аналогичным образом можно получить предельные гибкости для других материалов: - для дерева (сосна) - для чугуна Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде:
Таким образом, формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня, только в том случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен. В случае, когда формула Эйлера для критических напряжений (10.9) неприменима, критические напряжения определяются по эмпирической формуле, предложенной Ясинским, на основе опытов, проведенных рядом исследователей. Формула Ясинского имеет вид: для стали - σ;кр = а – bλ;; для чугуна - σ;кр= а – bλ + сλ;2, где а, b, c – коэффициенты, зависящие от свойств материала и измеряющиеся в единицах напряжения. Например, для стали Ст3 а = 310 МПа, b = 1,14 МПа (таблица 10.1). Таблица 10.1
|

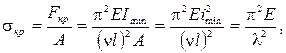 (10.9)
(10.9)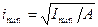 – геометрическая характеристика поперечного сечения, называемая минимальным радиусом инерции;
– геометрическая характеристика поперечного сечения, называемая минимальным радиусом инерции; 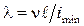 – безразмерная геометрическая характеристика, называемая гибкостью сжатого стержня, предложенная Феликсом Станиславовичем Ясинским (1856 – 1899 гг.).
– безразмерная геометрическая характеристика, называемая гибкостью сжатого стержня, предложенная Феликсом Станиславовичем Ясинским (1856 – 1899 гг.). , то есть
, то есть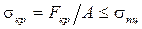 .
.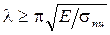 .
.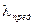 и назовем предельной гибкостью. Тогда
и назовем предельной гибкостью. Тогда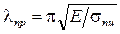 .
.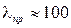 .
.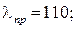
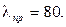
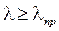 .
.


