Основные определения и гипотезы
Изгиб – это такой вид деформации бруса, при котором в его сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным. Брус, работающий преимущественно на изгиб, называется балкой. Если поперечные силы не возникают, изгиб называется чистым. Изгиб называется плоским, если все нагрузки и реакции связей действуют в одной плоскости. Ограничимся рассмотрением балок с прямолинейной продольной осью, поперечные сечения которых имеют, по меньшей мере, одну ось симметрии. Как известно ось симметрии и перпендикулярная ей центральная ось являются главными центральными осями сечения. Плоскость, проходящая через продольную ось балки и одну из главных центральных осей его поперечного сечения, называют главной плоскостью балки. В случае если силовая плоскость, то есть плоскость действия нагрузок, совпадает с одной из главных плоскостей, имеет место прямой изгиб балки. При прямом изгибе деформация происходит в силовой плоскости, то есть в этой плоскости располагается ось изогнутой балки. Для упрощения вывода формулы нормальных напряжений при изгибе в сопротивлении материалов используется ряд гипотез, справедливость которых подтверждается экспериментально. Содержание этих гипотез сводится к следующему: 1) продольные волокна при изгибе балок не давятдруг на друга (гипотеза отсутствия боковых давлений); 2) по ширине поперечного сечения балки нормальные напряжения не изменяются (гипотеза постоянства нормальных напряжений по ширине); 3) поперечные сечения поворачиваются, но не искривляются (гипотеза плоских сечений); 4) поперечная сила не оказывает влияния на нормальные напряжения, действующие в направлении геометрической оси балки. Гипотеза об отсутствии боковых давлений между продольными волокнами дает основание пользоваться формулой закона Гука:
справедливой для линейного напряженного состояния, когда главные напряжения σ2 = σ3 = 0. Гипотеза постоянства нормальных напряжений по ширине позволяет заключить, что величина нормальных напряжений не будет зависеть от координаты z (рис. 5.1).
Третья из отмеченных выше гипотез (гипотеза плоских сечений) дает возможность установить зависимость гипотетических деформаций «волокон» балки от их удаления от нейтральной оси (на нейтральной оси, по определению, линейные деформации и соответственно нормальные напряжения равны нулю). Наконец, четвертая гипотеза дает основание выполнить исследование нормальных напряжений без учета поперечной силы, как при чистом плоском изгибе. Аналитическое решение поставленной выше задачи показывает, что в произвольной точке поперечного сечения прямолинейного участка бруса нормальные напряжения определяются по формуле:
где Мz - изгибающий момент в поперечном сечении бруса; y – расстояние от главной центральной оси инерции z до точки, в которой определяется нормальное напряжение; Iz - осевой момент инерции поперечного сечения бруса относительно главной центральной оси z. Согласно формуле (5.2) нормальные напряжения по высоте поперечного сечения распределяются по линейному закону (см. рис. 5.1).
|

 , (5.1)
, (5.1)
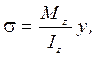 (5.2)
(5.2)


