Характеристики упругости
Деформация изотропного тела в упругой области может быть полностью описана, если известны упругие характеристики данного материала (упругие постоянные): модуль нормальной упругости Е, модуль сдвига G и коэффициент поперечной упругой деформации μ;. Модуль нормальной упругости характеризует сопротивляемость материала в упругой области деформации растяжения или сжатия. При постоянной температуре модуль нормальной упругости для данного материала, как при растяжении, так и при сжатии имеет практически одинаковую величину. Эта упругая характеристика материала входит, например, в формулу закона Гука при растяжении и сжатии для определения абсолютного удлинения (укорочения) ∆l или относительной линейной деформации ε; стержня где N - внутреннее осевое усилие; s - нормальное напряжение); l - длина стержня или его участка, в пределах которого определяется деформация; А - площадь поперечного сечения стержня. Произведение ЕА называется жесткостью поперечного сечения при растяжении или сжатии. Если тело испытывает упругопластические деформации, то зависимость между ∆l и N становится более сложной и закон Гука теряет силу. Из формул (4.1) можно экспериментально определить модуль нормальной упругости определяя деформацию ∆l (или ε;), соответствующую усилию N (или напряжению σ;). Как следует из формул (4.2), Е имеет размерность напряжения, 1 Н/м2 = 1 Па. Значения характеристик упругости для ряда конструкционных материалов приведены в таблице 4 Приложения. Модуль касательной упругости (модуль сдвига, модуль упругости второго рода) характеризует сопротивляемость материала деформации сдвига в упругой области. Запишем закон Гука при кручении:
где φ; - угол закручивания (γ; - относительный угол сдвига); Т - крутящий момент (τ; - касательное напряжение); l - длина стержня или участка, в пределах которого определяется деформация; Ip - полярный момент инерции поперечного сечения. Крутящий момент и полярный момент инерции в пределах данного участка должны быть постоянными. Произведение GIp называется жесткостью сечения при кручении. Аналогично растяжению, из формул (4.3) можно вычислить модуль сдвига для материала образца
Модуль G имеет размерность напряжения. Напомним, что для круглого сплошного сечения Третья упругая постоянная материала - коэффициент поперечной упругой деформации μ; (коэффициент Пуассона). Он устанавливает связьмежду относительной поперечной и относительной продольной деформациями в упругой области при линейном напряженном состоянии (растяжении или сжатии) (рис. 4.1).
Абсолютная поперечная деформация стержня определяется как разность его поперечных размеров до и после деформации: ∆a= a – a1; ∆в= в – в1. Относительная поперечная деформация стержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру. Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова: Коэффициент Пуассона равен абсолютной величине отношения поперечной деформации к продольной
Коэффициент Пуассона – безразмерная величина. Так как продольная и поперечная деформация для большинства конструкционных материалов имеют противоположные знаки, можем записать
Для изотропных материалов коэффициент Пуассона лежит в пределах от 0 до 0,5 (для пробкового дерева - µ ≈ 0; сталь - µ ≈ 0,3; каучук - µ ≈ 0,5). Кроме того, величину коэффициента Пуассона можно оценить из известного аналитического соотношения между Е, G и μ;:
Выражение (4.5) показывает, что из трёх постоянных, характеризующих упругие свойства изотропного материала, независимыми могут быть только две, так как любую третью можно определить, зная две другие упругие постоянные. Так, из формулы (4.5) следует
|

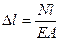 или
или  , (4.1)
, (4.1) или
или  ), (4.2)
), (4.2)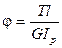 (или
(или 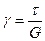 ), (4.3)
), (4.3) или
или  .
. .
.



 (4.4)
(4.4) или, учитывая, что, согласно закону Гука,
или, учитывая, что, согласно закону Гука, 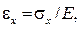 получим
получим
 . (4.5)
. (4.5)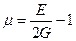 .
.


