Возможные решения задач
Класс Задача 1. Толкание ядра При стандартном решении этой задачи получается парадоксальный ответ – скорость в заданный момент времени оказывается больше начальной. Поэтому важной частью решения этой задачи является анализ полученных результатов!!!!. Если систему координат связать со спортсменом толкателем, то законы движения ядра будут определяться следующими уравнениями:
где
Так как это значение меньше указанных в условии 3 секунд, то скорость ядра в момент времени
а находиться ядро будет на расстоянии
от спортсмена. Критерии оценивания решения: 2 балла – записаны законы движения x (t) и y (t) [пп (1) и (2)]; 2 балла – получено выражение для момента времени приземления tкон [п.(3)]; 3 балла – определена скорость в момент 3 секунды [п. (4)]; 3 балла – вычислена дальность полета [ п. (5)]; Задача 2. Падение гантели . Обозначим скорость верхнего шарика
где потенциальная энергия отсчитывается от положения верхнего шарика в начальный момент времени. Сокращая массу шариков, получим:
Так как стержень жесткий, то проекции скоростей шариков на линию стержня должны быть равны:
Из уравнений (2) и (3) находим следующее выражение для скорости нижнего шара:
Подставляя
Критерии оценивания решения: 3 балла – записаны закон сохранения энергии x (t) и y (t) [п (1)]; 4 балла – получена связь скоростей [п.(3)]; 2 балла – записано выражение квадрата скорости нижнего шара [п. (4)]; 1 балл – вычислена искомая скорость [ п. (5)]; Задача 3. Как измерить прочность лески?
откуда можно выразить модуль силы
Постепенно натягивая леску, мы увеличиваем угол Критерии оценивания решения: 4 балла. Идея о нагрузке, действующей под углом к леске 4 балла Получение расчетной формулы (1) -. 2 балла Замечание о том, что при начальном разрыве леску надо сложить вдвое. Задача 4. Два теплых шара. Температура не будет одинаковой и более нагретым окажется шар, подвешенный на нити. Различие будет связано с поведением центров масс шаров. При нагревании шаров их объемы увеличиваются. В этом случае высота центра масс шара, лежащего на поверхности, увеличится, а центр масс подвешенного шара опустится. Таким образом, потенциальная энергия первого шара возрастет, а второго – уменьшится. Так как и в том и другом случае полная энергия системы остаётся постоянной, то на собственно нагрев шаров идёт различное количество энергии. Больше энергии, идущей на нагревание, будет передано подвешенному шару. Соответственно и температура его вырастет больше. Критерии оценивания решения: 3 балла - Привлечение эффекта теплового расширения шаров при нагревании. 3 балла -Вывод о разнонаправленном движении центров масс шаров. 4 балла - Применение закона сохранения энергии. Задача 5. Чему равно сопротивление цепи? Обозначим сопротивление между точками A и B для n звеньев
Решая это квадратное уравнение и отбирая физически осмысленный корень, получим:
Критерии оценивания решения: 6 баллов -Предложение эквивалентной схемы. 2 балла - Получение формулы (2) -. 2 балла - Вывод конечной формулы и численного результата. XLV Всероссийская олимпиада школьников по физике. Муниципальный этап.
|

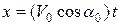 , (1)
, (1) , (2)
, (2) - модуль начальной скорости,
- модуль начальной скорости,  - начальный угол траектории движения ядра к горизонту. Ядро приземлится в момент времени:
- начальный угол траектории движения ядра к горизонту. Ядро приземлится в момент времени: . (3)
. (3) с будет равна нулю:
с будет равна нулю: (4)
(4) (5)
(5) , а скорость нижнего шарика
, а скорость нижнего шарика  . Согласно закону сохранения энергии можно записать:
. Согласно закону сохранения энергии можно записать: (1)
(1) (2)
(2) (3)
(3) (4)
(4) в это выражение, найдем искомую скорость:
в это выражение, найдем искомую скорость: (5)
(5)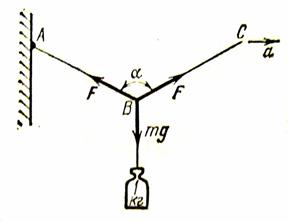 Подвесим гирю на леску так, как это показано на рисунке, а затем потянем леску в направлении, указанном стрелкой a. Между силами
Подвесим гирю на леску так, как это показано на рисунке, а затем потянем леску в направлении, указанном стрелкой a. Между силами  и
и 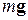 существует соотношение:
существует соотношение:
 (1)
(1)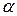 , в результате чего возрастает сила натяжения
, в результате чего возрастает сила натяжения  . Замерив с помощью транспортира критический угол, при котором наступает разрыв лески, можно подсчитать допустимую нагрузку. Если леска разрывается даже при нулевом угле, её следует сложить в двое и заново проделать описанную операцию, не забывая разделить конечный результат на два.
. Замерив с помощью транспортира критический угол, при котором наступает разрыв лески, можно подсчитать допустимую нагрузку. Если леска разрывается даже при нулевом угле, её следует сложить в двое и заново проделать описанную операцию, не забывая разделить конечный результат на два. . Тогда можно записать следующее рекуррентное соотношение:
. Тогда можно записать следующее рекуррентное соотношение: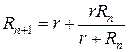 (1)
(1)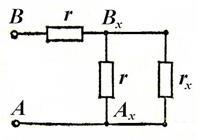 Сопротивление самого первого звена
Сопротивление самого первого звена  . Очевидно, что сопротивление каждого следующего звена для любого n меньше предыдущего, так как при параллельном подсоединении нового звена сопротивление между точками падает. С другой стороны эта последовательность ограничена снизу значением
. Очевидно, что сопротивление каждого следующего звена для любого n меньше предыдущего, так как при параллельном подсоединении нового звена сопротивление между точками падает. С другой стороны эта последовательность ограничена снизу значением  . Обозначим сопротивление всей сети как
. Обозначим сопротивление всей сети как  . Так как цепь бесконечная, то сопротивление цепи за точками
. Так как цепь бесконечная, то сопротивление цепи за точками  ,
,  тоже равно
тоже равно  (2)
(2) (3)
(3)


