ВВЕДЕНИЕ. 1°. Calculaţi valoarea expresiei , dacă . А B C D –11
1°. Calculaţi valoarea expresiei
2°. Arătaţi expresia identică egală cu
3°. Calculaţi valoarea expresiei:
4°. Calculaţi valoarea expresiei
5°. Arătaţi expresia identică egală cu
1°. Scrieţi polinomul
2°. Calculaţi valoarea polinomului
3°. Scrieţi polinomul
4°. Calculaţi suma, diferenţa şi produsul polinoamelor:
b)
b)
1°. Scrieţi polinomul
2°. Calculaţi valoarea polinomului
3°. Scrieţi polinomul
4°. Calculaţi suma, diferenţa şi produsul polinoamelor:
b)
b)
1°. Ridicaţi la pătrat binomul:
2°. Aflaţi produsul expresiilor:
3°. Scrieţi în formă de polinom expresia:
4°. Aduceţi la forma mai simplă expresia:
5°. Descompuneţi în factori polinomul:
a)
b)
a)
1°. Ridicaţi la pătrat binomul:
2°. Aflaţi produsul expresiilor:
3°. Scrieţi în formă de polinom expresia:
4°. Aduceţi la forma mai simplă expresia:
5°. Descompuneţi în factori polinomul:
a)
b)
a)
1°. Aflaţi valoarea funcţiei
2°. Pentru care valoare a argumentului funcţia
3°. Care din punctele date aparţin graficului funcţiei
4°. Aflaţi domeniul de definiţie al funcţiei:
5°. Trece oare graficul funcţiei
a) b) c)
1°. Aflaţi valoarea funcţiei
2°. Pentru care valoare a argumentului funcţia
3°. Care din punctele date aparţin graficului funcţiei
4°. Aflaţi domeniul de definiţie al funcţiei:
5°. Trece oare graficul funcţiei
a) b) c)
1°. Rezolvaţi sistemul de ecuaţii folosind metoda substituţiei:
2°. Rezolvaţi sistemul de ecuaţii folosind metoda adunării:
3°. Rezolvaţi sistemul de ecuaţii folosind metoda grafică:
a)
1°. Rezolvaţi sistemul de ecuaţii folosind metoda substituţiei:
2°. Rezolvaţi sistemul de ecuaţii folosind metoda adunării:
3°. Rezolvaţi sistemul de ecuaţii folosind metoda grafică:
a)
Lucrare anuală Varianta 1 1. De calculat valoarea expresiei
2. Cu care monom este egală expresia
3. De transformat expresia în polinom
4. Prin care din punctele date trece graficul ecuaţiei 5
5. De aflat rădăcinile ecuaţiei
6. De rezolvat sistemul de ecuaţii
7. Masa a două lingouri de cositor şi a 5 lingouri de plumb este de 33 kg, iar masa a 6 lingouri de cositor şi a 2 lingouri de plumb este de 34 kg. De aflat masa unui lingou de cositor şi a unui lingou de plumb. 8. Aduceți la forma mai simplă expresia: 9. Rezolvați sistemul de ecuații: Lucrare anuală Varianta 2 1. De calculat valoarea expresiei
2. Cu care monom este egală expresia
3. De transformat expresia în polinom
4. Prin care din punctele date trece graficul ecuaţiei 4
5. De aflat rădăcinile ecuaţiei
6. De rezolvat sistemul de ecuaţii
7. Pentru 5 kg de bomboane şi 4 kg de biscuiţi s-a plătit 320 grn. Cât costă 1 kg de bomboane şi cât costă 1 kg de biscuiţi, dacă 3 kg de bomboane sunt mai scumpe decât 2 kg de biscuiţi cu 60 grn. 8. Aduceți la forma mai simplă expresia: 9. Rezolvați sistemul de ecuații:
ВВЕДЕНИЕ Лабораторный практикум посвящен языку Си в его базовом варианте. Для исполнения данного цикла пригодна любая операционная среда и любая система программирования Си, так как те свойства языка, которые здесь изучаются, являются ядром языка и присутствуют во всех ее реализациях. Здесь рассматривается работа в операционной системе Windows XP и системе программирования Borland C. Описание каждой лабораторной работы начинается с разделов «Цель работы», «Краткие теоретические сведения» и «Примеры решения задач». Указанные в разделе «Краткие теоретические сведения» темы обязательно должны быть изучены по материалам лекционного курса и по литературе до начала лабораторной работы, а также должны быть разобраны все решения, приведенные в разделе «Примеры решения задач».
|

 , dacă
, dacă 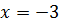 .
. .
.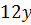


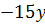
 .
. , dacă
, dacă 


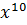


 . Scrieţi în forma standartă:
. Scrieţi în forma standartă:  .
. Calculaţi: a)
Calculaţi: a)  ; b)
; b)  .
. Aduceţi expresia
Aduceţi expresia  la forma mai simplă şi calculaţi valoarea ei pentru
la forma mai simplă şi calculaţi valoarea ei pentru  .
. 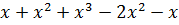 în formă standartă
în formă standartă



 , dacă
, dacă  .
. 





 . Scrieţi în formă de polinom: a)
. Scrieţi în formă de polinom: a)  ;
; .
. :
:
 . Rezolvaţi ecuaţiile: a)
. Rezolvaţi ecuaţiile: a)  ;
;
 în formă standartă
în formă standartă

 ;
; .
. :
:
 ;
;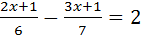




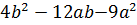
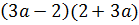 .
.


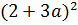
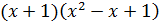
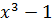












 . Aduceţi la forma mai simplă:
. Aduceţi la forma mai simplă: ; b)
; b)  .
. . Rezolvaţi ecuaţiile: a)
. Rezolvaţi ecuaţiile: a)  ;
; .
. . Scrieţi în formă de pătrat a binomului expresiile:
. Scrieţi în formă de pătrat a binomului expresiile: ; b)
; b)  .
.
 .
.

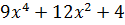
 ; b)
; b)  .
.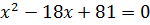 ;
; .
. ; b)
; b)  .
. , dacă valoarea argumentului este egală cu
, dacă valoarea argumentului este egală cu  .
.
 este egală cu –5.
este egală cu –5.
 .
.



 prin punctele A(–7;31), B(10; 49)?
prin punctele A(–7;31), B(10; 49)? cu axele de coordonate.
cu axele de coordonate. ;
; ;
; .
. şi se intersectează cu graficul
şi se intersectează cu graficul  în punctul situat pe axa ordonatelor.
în punctul situat pe axa ordonatelor. .
.
 .
. cu axele de coordonate.
cu axele de coordonate. ;
; ;
;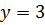 .
. şi se intersectează cu graficul
şi se intersectează cu graficul  în punctul situat pe axa ordonatelor.
în punctul situat pe axa ordonatelor.


 Care este preţul unui caiet şi a unui toc, dacă se ştie că pentru 12 caiete şi 8 tocuri s-a plătit 52grn., iar 7 caiete sunt mai scumpe decât 4 tocuri cu 13grn.
Care este preţul unui caiet şi a unui toc, dacă se ştie că pentru 12 caiete şi 8 tocuri s-a plătit 52grn., iar 7 caiete sunt mai scumpe decât 4 tocuri cu 13grn.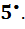 Rezolvaţi sistemul de ecuaţii:
Rezolvaţi sistemul de ecuaţii: b)
b) 
 Din două oraşe distanţa dintre care este egală cu 52 km, în acelaş timp au pornit unul în întâmpinarea celuilalt doi biciclişti care s-au întâlnit peste 2 ore. Aflaţi viteza cu care se mişca fiecare biciclist, dacă ştim, că al doilea timp de 3 ore a parcurs cu 18 km mai mult decât primul în 2 ore.
Din două oraşe distanţa dintre care este egală cu 52 km, în acelaş timp au pornit unul în întâmpinarea celuilalt doi biciclişti care s-au întâlnit peste 2 ore. Aflaţi viteza cu care se mişca fiecare biciclist, dacă ştim, că al doilea timp de 3 ore a parcurs cu 18 km mai mult decât primul în 2 ore.


 b)
b) 
 .
. ?
?

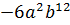

 .
.



 ?
?



 .
.




 .
.
 .
. ?
?

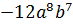

 .
.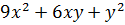



 ?
?



 .
.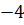


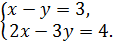




 .
.



