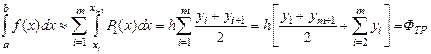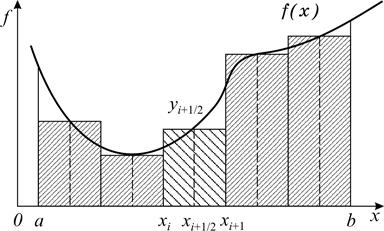
Формула среднихФормула средних получается, если на каждом i -м отрезке взять один центральный узел xi +1/2 = (xi + xi +1)/2, соответствующий середине отрезка. Функция на каждом отрезке аппроксимируется многочленом нулевой степени (константой) P 0(x) = yi +1/2 = f (xi +1/2). Заменяя площадь криволинейной фигуры площадью прямоугольника высотой yi +1/2 и основанием h, получим формулу средних (рис. 12.1):
Рис. 12.1
Формула трапеций Формула трапеций получается при аппроксимации функции f (x)на каждом отрезке [ xi, xi +1]интерполяционным многочленом первого порядка, т.е. прямой, проходящей через точки
Рис. 12.2
Порядок выполнения работы 1. Изучить теоретические сведения. 2. Ответить на контрольные вопросы. 3. Выполнить задание. Контрольные вопросы 1. Почему при программировании формулы трапеций и прямоугольников индексированные переменные xi и f(xi) можно заменить простыми переменными? 2. Почему начальное значение суммы по формуле трапеций принимается не равным нулю, а по формуле прямоугольников - равное нулю? 3. Какой метод при одном и том же значении n дает лучшее приближение? 4. В чем состоят преимущества использования операторов цикла в программах?
|
.
, 
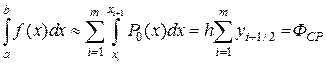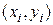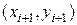. Площадь криволинейной фигуры заменяется площадью трапеции с основаниями 
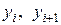и высотой h (рис.12.2):
