Краткая теория. Для определения спектральных характеристик светофильтров, как правило, проводят измерения спектральных зависимостей коэффициентов отражения и пропускания
Для определения спектральных характеристик светофильтров, как правило, проводят измерения спектральных зависимостей коэффициентов отражения и пропускания исследуемых образцов в выбранной области спектра. Энергетическим коэффициентом отражения R называется отношение модуля нормальной составляющей вектора Пойнтинга отраженной волны Энергетическим коэффициентом пропускания T называется отношение модуля нормальной составляющей вектора Пойнтинга прошедшей (преломленной) волны
где
(n 1 и n 2 – абсолютные показатели преломления сред). Коэффициенты R и T, отнесенные к фиксированной длине волны, называются монохроматическими. Учитывая, что реально измеряемыми в оптическом диапазоне являются средние значения векторов поля, соотношения (13.1) и (13.2) можно записать иначе:
где Iпд, Iот и Iпр – интенсивности падающей, отраженной и преломленной волн. Если рассматривать нормальное падение волны на границу раздела сред (будем считать, что в дальнейшем это условие всегда выполняется), т.е. αпд = αпр = 0, то соотношение (13.4) можно записать иначе
где I 0 = Iпд; n – относительный показатель преломления. Предположим, что поглощением волны в исследуемом образце можно пренебречь, тогда по закону сохранения энергии
Если поглощением пренебречь нельзя, то при распространении волны в среде ее интенсивность уменьшается экспоненциально, по закону Бугера
где I 0 – интенсивность падающей волны; I – интенсивность волны, прошедшей слой вещества толщиной d; α; ‑ показатель поглощения вещества. Из (13.7) следует, что α; имеет в СИ размерность м–1 и численно равен величине, обратной толщине слоя вещества, при прохождении которого интенсивность волны убывает в e раз. С учетом поглощения закон сохранения энергии (13.6) следует записать иначе:
где Зависимости коэффициентов отражения, пропускания и поглощения от длины волны часто называют спектрами отражения, пропускания и поглощения (под спектром поглощения, как правило, понимают спектральную зависимость не коэффициента поглощения K, а показателя поглощения α;). Наряду с коэффициентом пропуская T, для описания прозрачности вещества используют связанную с ним величину – оптическую плотность вещества D
при изменении T от 0 до 1 D изменяется от ¥ до 0. При экспериментальных измерениях дело, как правило, приходится иметь с плоскопараллельными образцами. Рассмотрим сначала два частных случая: в первом случае поглощением исследуемого образца можно пренебречь (α; = 0); во втором – отражением от поверхности образца можно пренебречь (R = 0). Если поглощение пренебрежимо мало, то в соответствии с (13.6) для определения спектральных характеристик образца достаточно измерить либо T = T (λ;), либо R = R (λ;). Пусть на плоскопараллельную пластину нормально падает узкий луч интенсивностью I 0. На рис. 13.1 представлена схема прохождения луча через пластину (отклонение от нормального падения луча на рис. 13.1 условно и вызвано необходимостью построения наглядной схемы). Рис. 13.1. Схема прохождения светового луча через плоскопараллельный образец без учета поглощения Как видно из приведенной схемы, реально при экспериментальных измерениях мы регистрируем не один прошедший или отраженный луч, а бесконечную совокупность лучей, возникших в результате многократных отражений от обеих поверхностей плоскопараллельного образца. Проведем расчет наблюдаемых R и T, предполагая, что пластинка достаточно толстая и, следовательно, прошедшие и отраженные лучи не интерферируют. Введем коэффициент однократного отражения r – френелевский коэффициент отражения. Как следует из схемы, приведенной на рис. 13.1,
Так как r по определению меньше 1, то, воспользовавшись формулой суммы бесконечно убывающей геометрической прогрессии, получим
Очевидно, что (13.10) и (13.11) удовлетворяют (13.6). (Левая часть последней формулы не противоречит (13.5), так как в данном случае падающая волна I0 и прошедшая волна Iпр распространяются в одной и той же среде.) Как известно, френелевский коэффициент отражения r связан с относительным показателем преломления n = n 2/ n 1 следующим соотношением (при нормальном падении луча):
Таким образом, измерив, например, спектр пропускания образца T (λ;), можно рассчитать остальные оптические характеристики:
Если n > 1, что всегда имеет место в нашем случае, в формуле (13.15) необходимо взять знак плюс. Рассмотрим второй частный случай, когда потерями на отражение можно пренебречь. В этом приближении схема прохождения луча через образец существенно упрощается: отражения нет, через пластину проходит один луч и в соответствии с (13.8) имеем
В этом случае, измерив спектр пропускания T (λ;), можно рассчитать оптическую плотность D(λ) по формуле (13.9), а воспользовавшись законом Бугера (13.7) – спектр поглощения образца α;(λ;) (или К(λ))
где d – толщина образца. Рассмотренные два частных случая дают приближенные решения задачи о нахождении спектральных характеристик плоскопараллельного образца, для ее строго решения необходимо учесть отражение и поглощение волны. Корректные результаты можно получить, измеряя для каждого образца спектр отражения и спектр пропускания. Действительно, повторив рассуждения по схеме на рис. 13.1, но уже с учетом поглощения (α; ¹ 0), можно получить следующую систему уравнений:
С помощью подстановки
|

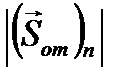 к модулю нормальной составляющей вектора Пойнтинга падающей волны
к модулю нормальной составляющей вектора Пойнтинга падающей волны 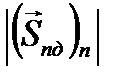 .
.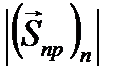 к модулю нормальной составляющей вектора Пойнтинга падающей волны
к модулю нормальной составляющей вектора Пойнтинга падающей волны  характеризует плотность потока энергии электромагнитной волны и имеет размерность Вт/м2).
характеризует плотность потока энергии электромагнитной волны и имеет размерность Вт/м2).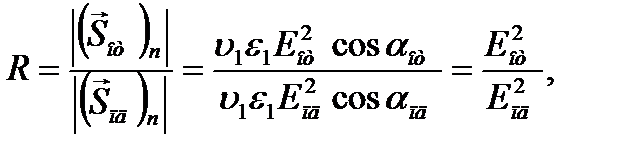 (13.1)
(13.1) , (13.2)
, (13.2)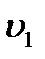 и
и  – скорости падающей и преломленной волны; ε1 и ε2 диэлектрические проницаемости сред, в которых распространяются падающая и преломленная волны; Eпд, Eот и Eпр – модули векторов напряженности электрического поля падающей, отраженной и преломленной волн; αпд , αот и αпр – углы падения, отражения и преломления; при этом было учтено, что в соответствии с законами отражения и преломления
– скорости падающей и преломленной волны; ε1 и ε2 диэлектрические проницаемости сред, в которых распространяются падающая и преломленная волны; Eпд, Eот и Eпр – модули векторов напряженности электрического поля падающей, отраженной и преломленной волн; αпд , αот и αпр – углы падения, отражения и преломления; при этом было учтено, что в соответствии с законами отражения и преломления 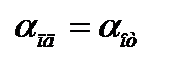 ,
,
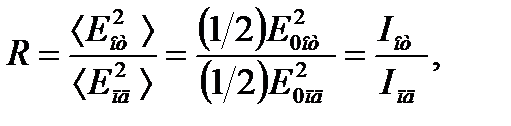 (13.3)
(13.3)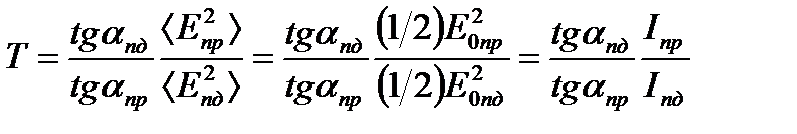 , (13.4)
, (13.4)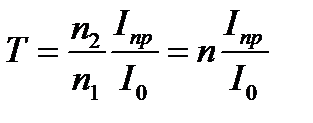 , (13.5)
, (13.5) . (13.6)
. (13.6)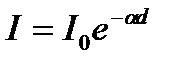 , (13.7)
, (13.7) , (13.8)
, (13.8)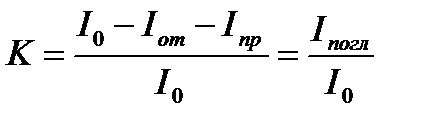 – коэффициент поглощения вещества, безразмерная величина, характеризующая долю поглощенной энергии.
– коэффициент поглощения вещества, безразмерная величина, характеризующая долю поглощенной энергии.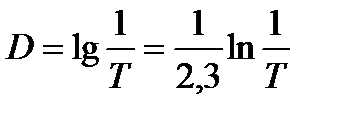 , (13.9)
, (13.9)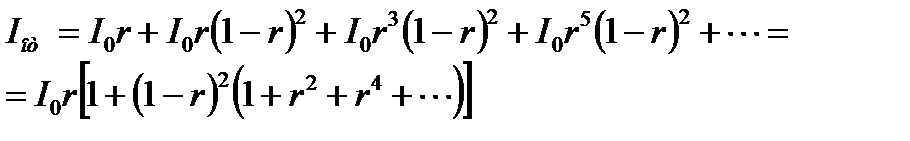
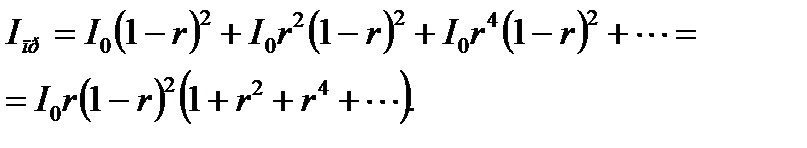
 и, следовательно,
и, следовательно, (13.10)
(13.10)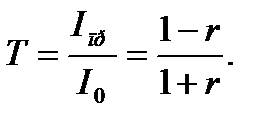 (13.11)
(13.11)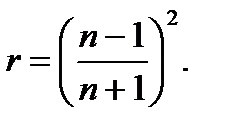 (13.12)
(13.12)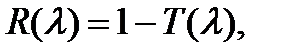 (13.13)
(13.13)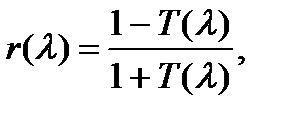 (13.14)
(13.14) (13.15)
(13.15) . (13.16)
. (13.16)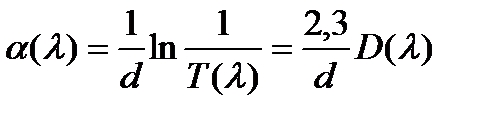 , (13.17)
, (13.17)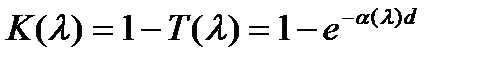 , (13.18)
, (13.18)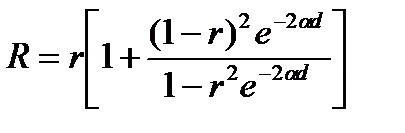 , (13.19)
, (13.19)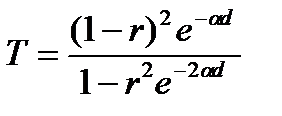 . (13.20)
. (13.20) нетрудно получить известное решение этой системы уравнений, т.е.
нетрудно получить известное решение этой системы уравнений, т.е.  ,
,  , а затем
, а затем 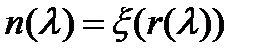 , но эти расчеты выходят за рамки данной лабораторной работы.
, но эти расчеты выходят за рамки данной лабораторной работы.


