Краткая теория. Выпуклая поверхность стеклянной линзы с большим радиусом кривизны соприкасается в некоторой точке с гладкой поверхностью стеклянной плоскопараллельной
Выпуклая поверхность стеклянной линзы с большим радиусом кривизны соприкасается в некоторой точке с гладкой поверхностью стеклянной плоскопараллельной пластинки так, что между ними остается воздушная прослойка, которая постепенно утолщающаяся от точки соприкосновения к краям. Если на такую систему падает параллельный пучок монохроматического света, то лучи отраженные от нижней поверхности линзы и верхней поверхности плоскопараллельной пластинки будут интерферировать между собой.
Рис. 14.1. Кольца Ньютона
При этом темные полосы в отраженном свете будут соответствовать светлым полосам в прошедшем свете и наоборот. В отраженном свете в центре картины будет находиться минимум. Таким образом, отраженный и прошедший свет взаимно дополняют друг друга: при их наложении образуется равномерно освещенная окружность. Рассмотрим описанное явление подробнее (рис. 14.2). Некоторый луч 1 падает на воздушную прослойку в точку C, частично отражается от верхней границы, а частично проходит и отражается от её нижней границы в точке B, после чего выходит из неё в точке A. Рис. 14.2 Ход лучей в воздушной прослойке
В эту же точку падает другой луч 2, который частично отражается. Отраженные лучи 1' и 2' являются когерентными и при наложении интерферируют между собой. Для прошедшего света рассуждения будут выглядеть аналогичным образом. Рассчитаем размеры колец Ньютона. При вычислении разности хода можно пренебречь небольшими отклонениями лучей, проходящих в тонком воздушном зазоре. Геометрическая разность хода между интерферирующими лучами (рис. 14.3) равна 2 d (показатель преломления среды n возд=1,0), где d – толщина воздушного зазора в данном месте.
Рис. 14.3 К расчету радиуса колец Ньютона R – радиус кривизны поверхности линзы (ОО’); О – точка соприкосновения сферичной поверхности с плоской поверхностью стеклянной пластины; r – радиус Кольца Ньютона.
Выразим зависимость d от расстояния r до радиуса, лежащего на прямой ОО'. Из рис. 14.3 имеем r=R2 – (R – d)2=2Rd – d2, где R – радиус кривизны выпуклой поверхности линзы. Так как 2 R» d, получим
При вычислении оптической разности хода интерферирующих лучей нужно учесть изменение фазы отраженной волны при отражении. Отражаясь от стеклянной пластинки, представляющей оптически более плотную среду, волна меняет фазу на противоположную, что эквивалентно изменению оптического хода на l/2. Следовательно, оптическая разность хода равна
∆=2d+l/2=r2/R+l/2. (14.2) В месте соприкосновения линзы и стеклянной пластинки остается очень тонкая воздушная прослойка, толщина которой намного меньше длины волны. Поэтому разность хода между лучами в этой точке определяется только потерей полуволны при отражении от пластинки ∆=l/2, и, следовательно, в центре интерференционной картины в отраженном свете мы будем наблюдать минимум интенсивности. Запишем условие минимума освещенности в интерференционной картине: ∆=(2m+1)l/2, где m = 0, 1, 2… – номер полосы. (14.3) Принимая во внимание (14.2), получим для радиуса r т темных колец в отраженном свете:
где m – номер темного кольца (минимум m -го порядка) Аналогично, для радиуса светлых колец в отраженном свете:
Измеряя радиусы светлых и темных колец, можно определить длину волны падающего света λ;, зная R, или, наоборот, по известному значению λ; найти R. Стоит отметить, что кольца Ньютона будут наблюдаться только на сравнительно небольшом расстоянии от точки O (рис. 14.3). Это связано с тем, что оптическая разность хода между лучами 1 и 2 должна быть меньше чем длина когерентности для используемого источника света. Так как обеспечить контакт в точке О трудно в следствии попадания пылинок, то пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец rk и ri, что позволяет исключить возможный зазор в точке О:
где k и i – порядки интерференционных колец, R – радиус кривизны выпуклой поверхности линзы. Формула (14.6) остается одной и той же как для интерференционных минимумов, так и для максимумов.
|



 . (14.1)
. (14.1)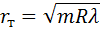 , (14.4)
, (14.4) . (14.5)
. (14.5) , (14.6)
, (14.6)


