Дисперсия призмы
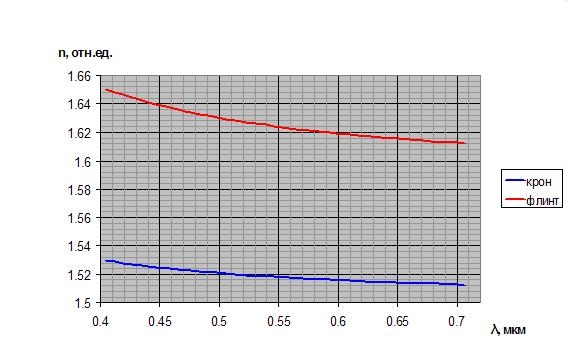
Явление дисперсии света впервые было изучено Исааком Ньютоном. Источником света служило небольшое круглое отверстие S в ставне экрана АВ, освещаемого лучами солнца. Когда перед отверстием устанавливалась призма Р1, то на экране С появлялась окрашенная полоска. Из этого пучка с помощью отверстия в экране выделялись узкие пучки определенной цветности (рис.15.1). Рис. 15.1 Прохождение света через призму Из этого опыта Ньютон сделал следующие выводы: 1. Белый свет является сложным светом, состоящим из цветных лучей. 2. Для лучей света различной цветности показатели преломления данного вещества различны; вследствие этого при отклонении призмой пучок белого света разлагается в спектр. 3. При соединении цветных лучей спектра вновь образуется белый свет. В процессе преломления в призме из пучка белого света выделяется множество цветных пучков, и каждому из них соответствует некоторая узкая область длин волн, заключенных в интервале между 400-800 нм. Показатель преломления вещества зависит от длины световой волны. Это и является причиной дисперсии света. На рис. 15.2 показан график зависимости показателя преломления от длины волны для призм изготовленных из флинта и крона.
Рис. 15.2 График зависимости показателя преломления от длины волны Рассмотрим соотношение, связывающие отношение показателей преломления вещества призмы и среды с преломляющим углом призмы наименьшего отклонения.
где n - показатель преломления вещества, из которого сделана призма; n0 – абсолютный показатель преломления среды; θ; – преломляющий угол призмы; αmin– угол наименьшего отклонения. Пусть n 0=1 (призма расположена в вакууме), тогда
Вычислим полный дифференциал dn:
Делим обе части на dl:
Величина
Угловая дисперсия тесно связана с линейной дисперсией. Линейная дисперсия тесно играет весьма важную роль в ряду характеристик, так как определяет возможность применения данного спектрального аппарата для фотографирования спектров различной сложности. Кроме того, линейная дисперсия характеризует реальную разрешающую способность прибора. Дисперсией спектрального прибора называется способность различно отклонять лучи разных длин волн так, чтобы они выходили из диспергирующего устройства под различными углами и фокусировались объективом в различных местах фотопластинки. Любой спектральный прибор должен иметь два объектива: первый (на входе) формирует параллельный пучок, второй (на выходе) формирует изображение на регистрирующее устройство. Поэтому возникает необходимость в количественной оценке линейной дисперсии. Если фокусное расстояние камерного объектива равно f 2, то имеем следующее соотношение:
, т.е. линейная дисперсия, равная угловой дисперсии, умноженной на фокусное расстояние камерного объектива, определяет линейный размер интервала спектра шириной в 1Ǻ. На рис. 15.3 показан ход лучей после прохождения призмы для двух длин волн: l и l+dl; dφ – угловое расстояние между ними; dl – соответствующееему линейное расстояние в фокальной плоскости объектива камеры. Рис.15.3 Определение линейной дисперсии призмы Из треугольника АВС видно, что если фокальная плоскость камерного объектива составляет с оптической осью объектива камеры угол ε, то расстояние на фотопластинке между спектральными линиями
Таким образом, в этом случае линейная дисперсия:
На практике для характеристик спектрографов вместо линейной дисперсии часто употребляют обратную ей величину, называемую обратной линейной дисперсией, определяющую величину интервала длин волн, измеряемого в ангстремах, приходящегося на 1 мм длины спектра:
|
,
.
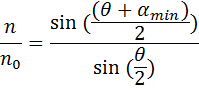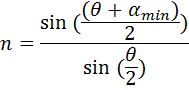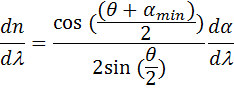
называется угловой дисперсией призмы, где dα; – разность углов выхода для двух лучей, длины волн которых отличаются на dl,рад/Ǻ.
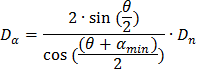
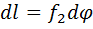или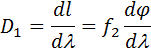 
.
.
.
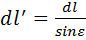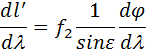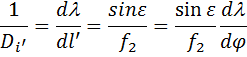