III. Раздел заданий для самостоятельной работы.
A. 1. Составить программу, в которой a. дано расстояние в сантиметрах. Найти число полных метров в нем; b. дана масса в килограммах. Найти число полных центнеров в ней; c. дана масса в килограммах. Найти число полных тонн в ней; d. дано расстояние в метрах. Найти число полных километров в нем; e. дан прямоугольник с размерами 543 2. Дано двузначное число. Получить число, образованное при перестановке цифр заданного числа. 3. Дано трехзначное число. Найти число, полученное при прочтении его цифр справа налево. 4. Дано целое число, большее 99. Найти третью от конца его цифру (так, если данное число 2345, то искомая цифра 3). 5. Дано четырехзначное число. Найти: a. сумму его цифр; b. произведение его цифр. 6. Составить программу, вычисляющую следующие выражения, в которых величины x,y,z вводятся с клавиатуры в диалоговом режиме: 6. 6. 6. 6. 6. 6.6.A = x + xy + xyz; B = xy / z + z / xy; 6.7.A = (1+x)2;B = sin (x +2zy); 6.8. A = arctg(1 - x 2);B = (x + y - z) 4; 6.9. A = (x – y)4y – ln z;B = lg(x4-yz); 6.10. A = lg(x4/4) + sin(yz); B = arcsin(y3- 3) + zln x;
7. Составить программу, вычисляющую следующие выражения, вводя новые переменные: 7.
7.
7. 7. 7. 7
7.
7.
7.
7.
8.Составить программу расчета значений функции
9. Составить программу расчета значений функции
10. Составить программу обмена значениями двух переменных величин. 11. Составить программу обмена значениями трёх переменных величин 11.1. 11.2. 12. Дано вещественное число 12.1. 12.2. 12.3 12.4
13.Вычислите несколько (n=3,4,5,6) длин волн
где масса электрона m=9.1 10-31 кг, его заряд е=1.6 10-19 Кл, постоянная Планка h=1.05 10-34 Дж с, диэлектрическая постоянная B. 1. Дано трехзначное число. a. В нем зачеркнули первую слева цифру и приписали её в конце. Найти полученное число. b. В нем зачеркнули последнюю справа цифру и приписали её в начале. Найти полученное число. c. Найти число, полученное при перестановке первой и второй цифр заданного числа. d. Найти число, полученное при перестановке второй и третьей цифр заданного числа. e. Получить 6 чисел, образованных при перестановке цифр заданного числа. 2. Из трехзначного числа a. Вычли его последнюю цифру. Когда результат разделили на 10, а к частному слева приписали последнюю цифру числа b. Вычли его последнюю цифру. Когда результат разделили на 10, а к частному слева приписали последнюю цифру числа 3. В трехзначном числе a. Зачеркнули первую цифру. Когда оставшееся число умножили на 10, а произведение сложили с первой цифрой числа b. Зачеркнули первую цифру. Когда полученное число умножили на 10, а произведение сложили с первой цифрой числа c. Зачеркнули его вторую цифру. Когда к образованному при этом двузначному числу слева приписали вторую цифру числа d. Зачеркнули его вторую цифру. Когда к образованному при этом двузначному числу слева приписали вторую цифру числа e. Зачеркнули его вторую цифру. Когда к образованному при этом двузначному числу справа приписали вторую цифру числа f. Зачеркнули его вторую цифру. Когда к образованному при этом двузначному числу справа приписали вторую цифру числа g. Зачеркнули его последнюю цифру. Когда в оставшемся двузначном числе переставили цифры, а затем приписали к ним слева последнюю цифру числа h. Зачеркнули его последнюю цифру. Когда в оставшемся двузначном числе переставили цифры, а затем приписали к ним слева последнюю цифру числа 4. Дано четырехзначное число. a. Найти число, полученное при прочтении его цифр справа налево. b. Получить число, образуемое при перестановке двух первых и последних цифр заданного числа. Например, из числа 4566 получить 6645, из числа 7304 – 473. c. Получить число, образуемое при перестановке первой и второй, третьей и четвертой цифр заданного числа. Например, из числа 5434 получить 4543, из числа 7048 – 784. d. Получить число, образуемое при перестановке второй и третьей цифр заданного числа. Например, из числа 5084 получить 5804. 5. Даны целое число a. номер пары цифр, в которую входит b. двузначное число, образованное парой цифр, в которую входит c. 6. Даны целое число 7. Определить время приземления самолета в часах X, минутах Y и секундах Z. Известно, что самолет вылетел в X0 часов, Y0 минут и Z0 секунд и находился в воздухе Q секунд. Учесть переход времени на другие сутки. 8. С начала 1990 года по некоторый день прошло n месяцев и 2 дня (n≥1). Присвоить целочисленной величине 9. Часовая стрелка образует угол Y с лучом, проходящим через центр и через точку, соответствующую 12 часам на циферблате, 0<Y≤ 10. Даны целые числа 11. С начала суток часовая стрелка повернулась на Y градусов (0 12. С начала суток прошло a. сколько полных часов прошло с начала суток; b. сколько полных минут прошло с начала очередного часа; c. сколько полных секунд прошло с начала очередной минуты. 13. Составить программу, вычисляющую следующие выражения, в которых величины x,y,z вводятся с клавиатуры в диалоговом режиме: 2.
2. 2. 2. 2.
3.1.Составить программу вычисления площади треугольника по формулам: S1=a*ha/2; S2=b*hb/2; S3=c*hc/2;
S5=a*b*c/(4R); S6=p*r;
где a,b,c – стороны треугольника; hа, hb, hc – высоты, опущенные на стороны a,b,c, соответственно; p = (a+b+c)/2 – полупериметр; R,r – радиусы окружностей, описанной около треугольника и вписанной в него;
3.2.Дан треугольник со сторонами a,b,c. Составить программу вычисления его медиан, биссектрис и углов. 3.3.Треугольник задан величинами своих углов и радиусом описанной окружности. Составить программу вычисления сторон треугольника. 3.4.Треугольник задан координатами своих вершин (x1,y1), (x2,y2) и (x3,y3). Составить программу вычисления периметра и площади треугольника. 3.5.Треугольник задан координатами своих вершин (x1,y1), (x2,y2) и (x3,y3). Составить программу вычисления радиуса вписанной окружности. 3.6.Треугольник задан координатами своих вершин (x1,y1), (x2,y2) и (x3,y3). Составить программу вычисления радиуса описанной окружности. 3.7.Треугольник задан координатами своих вершин (x1,y1), (x2,y2) и (x3,y3). Составить программу вычисления углов треугольника. 3.8. Дана сторона квадрата. Найти его периметр. 3.9. Дана длина ребра куба. Найти объём куба и площадь его боковой поверхности. 3.10.Даны основания и высота равнобедренной трапеции. Найти её периметр. Даны основания трапеции и угол при большом основании. Найти площадь трапеции. 4.1. Используя таблицу данных о планетах Солнечной системы (см. работу 2), составить программу расчета ускорения свободного падения на каждой из планет, периоды обращения планет, предполагая, что их обращение вокруг Солнца происходит по круговой орбите и силы их притяжения к Солнцу. Результаты получить в абсолютных и относительных к параметрам Земли единицах и вывести в виде таблицы. Гравитационная постоянная равна G=6.67 Е-12. 4.2.Напишите программу решения квадратного уравнения ax2 + bx + c =0, используя формулы: Проведите расчеты в случае 4.3.При измерении сопротивлений при помощи моста Уитстона вычисления проводятся по формуле: Rx=R0 *z/(1-z), где z =l1/L – относительная длина реохорда. Абсолютная и относительная ошибки
Составить программу и сделать расчеты погрешностей для z=0.1...0.9.
4.4. Написать программу показывающая что значение выражения (1/3)*3 – 1 в Паскале не равно нулю. 4.5. Выведите на экран величину основания натуральных логарифмов (число е), не используя явно его цифры. Выведите число p не используя стандартную функцию Pi. 4.6. Вычислите выражение (x + 1/2)*(y + 7/10) – 3/4 сделав минимальное количество операций. 4.7. Присвоить целой переменной d первую цифру из дробной части положительного вещественного числа х (так, если х = 32.597, то d = 5). 4.8. Определить f - угол (в градусах) между положением часовой стрелки в начале суток и ее положением в h часов, m минут и s секунд (0≤h≤11, 0≤m, s≤59)
С. (В программах условные операторы и операторы цикла не использовать) 1. Даны два целых числа a и b. Если 2. Даны целые числа b, m (0< d. совпадут; e. расположатся перпендикулярно друг другу. 3. Определите, какой день недели приходится на 1 января для любого года XX и XXI вв. 1 января 1900 г. – Понедельник. 4. Дано целое число 5. Составьте программу определяющую день недели по дате.(см. с.3, с.4) 6. Составьте программу определяющую разницу в сутках между двумя датами.
|

 130 мм. Сколько квадратов со стороной 130 мм можно отрезать от него?
130 мм. Сколько квадратов со стороной 130 мм можно отрезать от него?










 ;
;



 и
и  при любых значениях
при любых значениях  и
и  .
. и
и  при любых значениях
при любых значениях  и
и  .
. по следующей схеме:
по следующей схеме: присвоить значение
присвоить значение 
 ,
,  присвоить значение
присвоить значение  за две операции; 12.5.
за две операции; 12.5.  за три операции; 12.9.
за три операции; 12.9.  за четыре операции;
за четыре операции; за три операции; 12.6
за три операции; 12.6 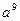 за четыре операции; 12.10
за четыре операции; 12.10  за четыре операции;
за четыре операции; за пять операций; 12.7.
за пять операций; 12.7.  за пять операций; 12.11
за пять операций; 12.11  за шесть операций;
за шесть операций; за шесть операций; 12.8
за шесть операций; 12.8  за шесть операций;
за шесть операций; спектральной серии Бальмера:
спектральной серии Бальмера:
 =8.85 10-12 Кл2/(Нм2), скорость света с=3 108 м/с.
=8.85 10-12 Кл2/(Нм2), скорость света с=3 108 м/с.
 . Найти число
. Найти число 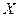 , то получилось число 654. Найти число
, то получилось число 654. Найти число  . По заданному
. По заданному  (
(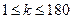 ) и последовательность цифр 10111213…9899, в которой выписаны подряд все двузначные числа. Определить:
) и последовательность цифр 10111213…9899, в которой выписаны подряд все двузначные числа. Определить: 1,2, …, 11 или 12 в зависимости от того, каким месяцем (январем, февралём и т.п.) является месяц этого дня. Например, при
1,2, …, 11 или 12 в зависимости от того, каким месяцем (январем, февралём и т.п.) является месяц этого дня. Например, при  значение
значение  . Определить значение угла для минутной стрелки, а также количество часов и полных минут.
. Определить значение угла для минутной стрелки, а также количество часов и полных минут. (0<
(0< 
 23, 0
23, 0  , 0
, 0  ), указывающие момент времени: “b часов, m минут, s секунд”. Определить угол в градусах между положением часовой стрелки в начале суток и в указанный момент времени.
), указывающие момент времени: “b часов, m минут, s секунд”. Определить угол в градусах между положением часовой стрелки в начале суток и в указанный момент времени. ,Y- вещественное число). Определить число полных часов и число полных минут, прошедших с начала суток.
,Y- вещественное число). Определить число полных часов и число полных минут, прошедших с начала суток. секунд. Определить:
секунд. Определить:





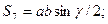

 углы, противолежащие сторонам a,b,c соответственно.
углы, противолежащие сторонам a,b,c соответственно. и
и 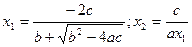

 делится на
делится на  или
или  . Присвоить целочисленной величине
. Присвоить целочисленной величине 


