II. Экспериментальный раздел работы
Пример 1. Напишем программу, в которой логическая переменная принимает значение true, если, случайным образом выбранная, точка с координатами (x,y) попадает внутрь кольца с центром в начале координат и радиусами 0.1 и 0.6, иначе - логическая переменная принимает значение false. #include <iostream.h> #include <conio.h> #include <stdlib.h> void main (void) { float x,y; bool p; //Ввод данных randomize(); x=rand()/10000.0; y=rand()/10000.0; cout<<"x="<<x<<" y="<<y<<endl; //Расчет p=((x*x + y*y)> 0.1) && ((x*x + y*y) < 0.6); //Вывод результата} cout<<"p="<<p; getch(); } Поэкспериментируйте с программой. Замените логическое выражение на p=!(((x*x + y*y)< 0.1) || ((x*x + y*y) > 0.6)); Основываясь на законах де Моргана, объясните полученные экспериментальные результаты. Пример 2. Составим программу, результатом работы которой будет удаление из двоичного представления данного натурального числа i-го бита.
#include <iostream.h> #include <conio.h> void main (void) { int n,x,y,z,k; //Ввод данных cout<<"Введите значение натурального числа n=?"<<endl; cin>>n; cout<<"Введите номер вычеркиваемого бита k=?"<<endl; cin>>k; //Расчет x=1 << k; y=~x; z=n & y; //Можно было написать z=n & ~(1 << k); //Вывод результата cout<<"x="<<x<<" y="<<y<<" z="<<z<<endl; getch(); } Необходимо разобраться с алгоритмом программы, провести тестовый расчет.
Пример 3. Дайте объяснение результатам следующей программы.
#include <iostream.h> #include <conio.h> void main (void) { cout<<(1365 & 2730)<<endl; cout<<(1365 | 2730)<<endl; cout<<(1365 ^ 2730)<<endl; cout<<(1365 & 0xFF)<<endl; cout<<(1365 & 0xFF0)<<endl; cout<<(1365 & 0xFF00)<<endl; getch(); }
Для объяснения полученных результатов переведите числа в двоичную систему счисления. Поэкспериментируйте с программой. Убедитесь, например, что -256 & 255 =0; -256 | 255 = -1; -256 ^ 255 = -1. Вспомните, что для представления отрицательных чисел в компьютере используется дополнительный код. Замените побитовые операции над числами логическими и сравните полученные результаты. Дайте объяснение путем выполнения данных операций без использования ЭВМ.
Пример 4. Составим программу определения наибольшего из двух чисел.
#include <iostream.h> #include <conio.h>
double Max(double a,double b) { if (a>b) return a; else return b; } void main (void) { double x,y,max; cout<<"Введите два числа x,y=?"; cin>>x>>y; cout<<"max="<<Max(x,y)<<endl; getch(); }
Разработайте алгоритм и составьте программу определения наибольшего числа из трех, четырех чисел. Используйте для ввода чисел генератор случайных чисел randomize(); rand. Проведите вычислительный эксперимент с программой. Пример 5. Проведите вычислительный эксперимент с программой, использующей оператор switch: #include <iostream.h> #include <conio.h> void main (void) { short month; cout<<"Введите номер месяца в году:"<<endl; cin>>month; switch (month) { case 1: cout<<"зимняя сессия";break; case 2: case 3: case 4: case 5: cout<<"весенний семестр";break; case 6: cout<<"летняя сессия";break; case 7:case 8: cout<<"летние каникулы";break; case 9:case 10: case 11:case 12: cout<<"осенний семестр";break; } getch(); } Ш. Раздел заданий для самостоятельной работы A. 1. Вычислить значение логического выражения при всех возможных значениях логических величин А и В: 1.1 А или В; А и В; В или С.; А или В и не С; А и не В или С; не А или не В; 1.2 А или не В;А и В или С; А и (А или не В); (не А или В) и В; не А и не В или А; 1.3 А и (не В или С);В или не(А и не В); В или не А и не В; не (не А и не В) или А; 1.4 не А и не В; не (не А или не В) или А; не (А и С) или В; А и (не (В или С)); 1.5 не (не А или не В) и В; А или не (А и В) или С; не А или А и (В или С); 1.6 (А или В и не С) и С; (не А или не В) и не С; (не А или не В) и (А или В); 1.7 А и В или А и С или не С; не (А или не В и С); А и не (В или не С);. 1.8 не (А или не В и С) или С; не (не А или В и С); не (А и не В или С) и В; 1.9 не (не А или В и С) или А; не (А и В) и (не А или не С); не (А и не В) или (А или не С); 2 Вычислить значения логических выражении: 2.1 2.2 ( 2.3 ( 2.4 2.5 2.6 (не ( 2.7 (не ( 2.8 2.9 2.10 ( 2.11 2.12 2.13 (не ( 2.14 (не ( 3 Записать условие, которое является истинным, когда 3.1 каждое из чисел А и В больше 100; 3.2 только одно из чисел А и В четное; 3.3 хотя бы одно из чисел А и В положительно; 3.4 каждое из чисел А, В, С кратно трем; 3.5 только одно из чисел А, В и С меньше 50; 3.6 хотя бы одно на чисел А, В, С отрицательно. 3.7 каждое из чисел X и У нечетное; 3.8 только одно из чисел X и У меньше 20; 3.9 хотя бы одно из чисел X и У равно нулю; 3.10 каждое из чисел X, У, Z отрицательное; 3.11 только одно из чисел X, Y и Z кратно пяти; 3.12 хотя бы одно из чисел X, Y, Z больше 100. 3.13 целое А кратно двум или трем; 3.14 целое А не кратно трем и оканчивается нулем. 3.15 целое N кратно пяти или семи; 4 Дано целое число. Определить: 4.1 является ли оно четным; 4.2 оканчивается ли оно цифрой 7; 4.3 оканчивается ли оно четной цифрой. Составное условие не использовать. 5 Дано натуральное число. Верно ли, что оно заканчивается нечетной цифрой? 6 Дано двузначное число. Определить: 6.1 какая из его цифр больше: первая или вторая; 6.2 одинаковы ли его цифры; 6.3 равен ли квадрат этого числа учетверенной сумме кубов его цифр. Например, для числа 48 ответ положительный, для числа 52-отрицательный. 6.4 является ли сумма его цифр двузначным числом; 6.5 больше ли числа А сумма его цифр; 6.6 кратна ли трем сумма его цифр; 6.7 кратна ли сумма его цифр числу А; 6.8 входят ли в него цифры А или В; 7 Даны три вещественных числа a, b, c. Проверить: а) выполняется ли неравенство а < b< c; б) выполняется ли неравенство b > а > с; в) имеется ли среди них хотя бы одна пара равных между собой чисел; г) сколько среди них отрицательных. 8. Даны два числа. Если квадратный корень из второго числа меньше первого числа, то увеличить второе число в пять раз. 9. Даны три целых числа. Вывести на экран те из них, которые являются четными. 11. Даны три вещественных числа. Возвести в квадрат те из них, значения которых неотрицательны. 12. Даны два вещественных числа. Условно принимая, что стандартной функции определения абсолютной величины числа нет, найти: а) полу сумму абсолютных величин заданных чисел; б) квадратный корень из произведения абсолютных величин заданных чисел. 13. Даны три вещественных числа. Вывести на экран: а) те из них, которые принадлежат интервалу (1,6 - 3,8); б) те из них, которые принадлежат интервалу (0,7-5,1). 14. Проверить, принадлежит ли число, введенное с клавиатуры, интервалу ( 15. Дано четырехзначное число. Определить: а) равна ли сумма двух первых его цифр сумме двух его последних цифр; б) кратна ли трем сумма его цифр; в) кратно ли четырем произведение его цифр; г) кратно ли произведение его цифр числу А; д) входит ли в него цифра 4; е) входит ли в него цифра В. ж) входят ли в него цифры 2 или 7; з) входят ли в него цифры 3, 6или 9. B. 1. Составьте программу проверки эквивалентности двух логических функций. Постройте соответствующие таблицы истинности(программно). 1.1. Проверьте что X → Y эквивалентна not (x) or y 1.2. Проверьте что X │ Y (Функция Шеффера) эквивалентна not (x) or not(y) 1.3. Проверьте что X ↓ Y (Функция Вебба, или стрелка Пирса) эквивалентна not (x) and not (y) 1.4. Дана некоторая логическая функция, например, (x→y)→z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.5. Дана логическая функция (x │ y) │ z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.6. Дана логическая функция (x ↓ y) ↓ z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.7. Дана логическая функция (x → y) and z. Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.8. Дана логическая функция not (x or not y and z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.9. Дана логическая функция x and not (y or not z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.10. Дана логическая функция not (not x or y and z). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 1.11. Дана логическая функция (x ↓ y) ↓ (z ↓ v). Постройте таблицу истинности данной функции. Преобразуйте эту формулу в эквивалентную ей. Составьте программу проверки эквивалентности этих двух логических формул. 2. Вывести на экран True при выполнении условия 2.1. х принадлежит отрезку [2,5] или [-1,1]; 2.2. x лежит вне отрезков [2,5] и [-1,1]; 2.3. только одно из чисел x, y и z положительно; 2.4. из чисел x, y и z только два равны между собой; 2.5. уравнение ax2+bx+c=0 не имеет вещественных корней; 2.6. a = max (a, b, c, d); 2.7. целые n и k имеют одинаковую чётность; 2.8. поля (г1, в1) и (г2, в2) шахматной доски имеют одинаковый цвет. 2.9. ферзь, расположенный на поле (г1, в1) шахматной доски, "бьет" поле(г2, в2). 2.10. число n нечетное.(Напишите свой вариант функции odd, возвращающей значение "Истина", если её целочисленный аргумент имеет нечетное значение). 3. Если целое число Мделится нацело на целое число N, то вывести на экран частное от деления, а в противном случае вывести сообщение "М на N нацело не делится". 4. Даны цифры двух десятичных целых чисел: трехзначного 4.1. цифры, составляющие сумму этих чисел; 4.2.цифры, составляющие разность этих чисел. 5. Дано натуральное число п (п < 9999). Выяснить, является ли оно палиндромом ("перевертышем"), с учетом четырех цифр, как, например, числа 7777, 8338, 0330 и т.п. (палиндромом называется число, десятичная запись которого читается одинаково слева направо и справа налево). 6. Даны вещественные числа a, b, c ( 7. Даны вещественные положительные числа a, b, c a. выяснить, существует ли треугольник со сторонами a, b, c. b. можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника. 8. В подъезде жилого дома имеется п квартир, пронумерованных подряд, начиная с номера a. Определить, является ли сумма номеров всех квартир четным числом. Формулу суммы членов арифметической прогрессии не использовать. 9. Случайным образом вводятся координаты точек. Определить, сколько из них попадет в круг радиусом R с центром в точке (a,b). 10. Даны два прямоугольники, стороны которых параллельны или перпендикулярны осям координат. Известны координаты левого нижнего угла каждого из них и длины их сторон. Один из прямоугольников назовем первым, другой — вторым. a. Определить, принадлежат ли все точки первого прямоугольника второму. b. Определить, принадлежат ли все точки одного из прямоугольников другому. c. Определить, пересекаются ли эти прямоугольники. 11. Даны два прямоугольника, стороны которых параллельны или перпендикулярны осям координат. Известны координаты левого нижнего угла каждого из них и длины их сторон. Один из прямоугольников назовем первым, другой — вторым. Найти координаты левого нижнего и правого верхнего углов минимального прямоугольника, содержащего указанные прямоугольники. 12. Определить, попадает ли точка с вводимыми координатами (x,y) внутрь прямоугольника, заданного уравнениями y=a, y=b, x=c, x=d (a>b, c>d). 13. Определить находится точка с координатами (x,y) выше или ниже прямой, заданной уравнением y=ax+b. 14. Определить находится точка с координатами (x,y) в кольце с радиусами R = 5, r = 3 с центром в точке (2,-1). 15. Является ли случайным образом введенный год високосным. У високосного года номер года делится на 4 или на 400, но не делится на 100. 16. Известны год и номер месяца рождения человека, а также год и номер месяца сегодняшнего дня (январь – 1 и т.д.). Определить возраст человека (число полных лет). В случае совпадения указанных месяцев считать, что прошел полный год. 17. Дано натуральное число п (1 18. Известны год и номер месяца рождения двух человек. Определить, возраст каждого человека (число полных лет). 19. Известны год, номер месяца и день рождения человека, а также год, номер месяца и номер текущего дня месяца (1 — январь и т.п.). Определить возраст человека (число полных лет). 20. Известны год и номер месяца рождении человека, а также год и номер месяца сегодняшнего дня (1 январь и т.п.). Определить возраст человека (число полных лет и число полных месяцев). При определении числа полных месяцев дни месяца не учитывать, а использовать разность между номерами месяцев. Например, если месяц рождения февраль, а текущий (сегодняшний) месяц май, то число полных месяцев равно трем независимо от дней рождения и сегодняшнего. 21. Дано натуральное число п (п < 9999). Выяснить, верно ли, что это число содержит ровно три одинаковые цифры, если оно записано четырьмя цифрами, как, например, числа 3363, 4844, 0300 и т.п. 22. Дано натуральное число п (п < 9999). Выяснить, различны ли все четыре цифры этого числа (если оно записано четырьмя цифрами). Например, в числе 3678 все цифры различны, в числе 0023 — нет. 23. Даны вещественные положительные числа a, b, c, x, у. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x и у. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия. 24. Работа светофора для пешеходов запрограммирована следующим образом: в начале каждого часа в течение трех минут горит зеленый сигнал, затем в течение двух минут — красный, в течение трех минут - опять зеленый и т.д. Дано вещественное число t, означающее время в минутах, прошедшее с начала очередного часа. Определить, сигнал какого цвета горит для пешеходов в этот момент. 25. Даны вещественные числа а, b, с ( 26. Даны две тройки вещественных чисел. В каждой тройке все числа различные. Найти среднее арифметическое средних чисел каждой тройки (средним назовем такое число в тройке, которое больше наименьшего из чисел данной тройки, но меньше наибольшего). 27. Даны целые числа х и у. Написать программу определения знака разности х – у. Саму разность при этом не вычислять. Разрешается сравнивать числа х и у с нулем, а между собой можно сравнивать только модули чисел х и у. 28. Считая, что стандартные функции sin и cos применимы только к аргументам из отрезка [0,p/2], вычислить у = sin x для произвольного числа х. 29. Даны числа a1, b1, c1, a2, b2, c2. Напечатать координаты точки пересечения прямых a1*x + b1*y = c1 и a2*x + b2*y = c2, либо сообщить, что эти прямые совпадают, не пересекаются или вовсе не существуют. 30. Даны числа a, b и c (a ≠ 0).Найти вещественные корни уравнения a x4+ b x2+ c=0. Если корней нет, то сообщить об этом. 31. Решить систему неравенств
c x > d. a, b, c, d вводятся с клавиатуры. 32. Даны три вещественных числа, Используя только два неполных условных оператора, определить: a. максимальное значение заданных чисел; b. минимальное значение заданных чисел. 33. Даны отрезки А,B,C. Составить программу для определения возможности построения треугольника и вида этого треугольника. 34. Даны координаты трех точек. Определить тип треугольника (равнобедренный, равносторонний, прямоугольный, разносторонний), вычислить его площадь и периметр. 35. Определить попадает ли точка с координатами (x,y) внутрь треугольника, заданного координатами (x1,y1), (x2,y2), (x3,y3). 36. Вводятся три числа: g – год, m – месяц, n – число. Найти номер этого дня в году. 37. Известны год и номер месяца рождения двух человек. Определить, возраст каждого человека (число полных лет). Определить, кто из них старше. 38. Известны год, номер месяца и день рождения человека, а также год, номер месяца и номер текущего дня месяца (1 — январь и т.п.). Определить возраст человека (число дней).Учитывать неправильность в вводе дат. Так если первое число "больше" второго должно выводится соответствующее предупреждение. 39. Поезд прибывает на станцию в а часов b минут и отправляется в с часов d минут. Пассажир пришел на платформу в п часов m минут. Будет ли поезд стоять на платформе? Числа а, b, с, d, п, т — целые, 0 < а 40. С начала 1990 года по некоторый день прошло п месяцев и 2 дня ( 41. Дата некоторого дня определяется двумя натуральными числами: т (порядковый номер месяца) и п (число). По заданным п и т определить: а) дату предыдущего дня (принять, что п и т не определяют 1 января); б) дату следующего дня (принять, что п и т не определяют 31 декабря). В обеих задачах принять также, что год не является високосным.
С. При решении задач (№ 1-14) необходимо использовать оператор выбора switch 1. Написать программу, которая бы переводила слова «ДОБРЫЙ ДЕНЬ» по выбору на один из пяти языков. 2. Найти остаток от деления целой части значения функции z=ln(x3+y3) на семь и в зависимости от его величины напечатать сообщение об одном из дней недели, пронумеровав их от 0 до 6. 3. Вычисления значения функции y= ax+bx2+cx3, если 1<=x<2, y= [a sin(x b)]c, если 2<=x<3,
4. Составить программу, которая в зависимости от порядкового номера дня недели (1, 2,..., 7) выводит на экран его название (понедельник, вторник,.... воскресенье). 5. Составить программу, которая в зависимости от порядкового номера месяца (1,2,.... 12) выводит на экран его название (январь, февраль,…, декабрь). 6. Составить программу, которая в зависимости от порядкового номера месяца (1,2, …, 12) выводит на экран количество дней в этом месяце. Рассмотреть 2 случая: a) год не является високосным (см. задачу 4.48); b) год високосный (информация об этом вводится с клавиатуры). 7. Мастям игральных карт условно присвоены следующие порядковые номера: масти "пики"—1,масти трефы - 2, масти "бубны" — 3, масти "червы" — 4. По заданному номеру масти т ( 8. Игральным картам условно присвоены следующие порядковые номера в зависимости от их достоинства: "валету" — 11, "даме" — 12, "королю" — 13, "тузу" 14. Порядковые номера остальных карт соответствуют их названиям ("шестерка", "девятка" и т.д.). По заданному номеру карты k ( 9. Дано целое число п (1 < п < 99), определяющее возраст человека (в годах). Для этого человека напечатать фразу “мне п лет ”, учитывая при этом, что при некоторых значениях п слово “лет” надо заменить на слово “год” или “года”. 10. В чемпионатe по футболу команде за выигрыш дается 3 очка, за проигрыш — 0, за ничью - 1. Известно количество очков, полученных командой за игру. Определить словесный результат игры (выигрыш, проигрыш или ничья). 11. В старояпонском календаре был принят 60-летний цикл, состоящий из пяти 12-летних подциклов. Подциклы обозначались названиями цветов: зеленый, красный, желтый, белый и черный. Внутри каждого подцикла годы носили названия животных: крыса, корова, тигр, заяц, дракон, змея, лошадь, овца, обезьяна, курица, собака и свинья. Например, 1984 год — год начала очередного цикла — назывался Годом Зеленой Крысы. Составить программу, которая по заданному номеру года нашей эры п печатает его название по старояпонскому календарю. Рассмотреть два случая: а) значение п ≥1984; б) значение п может быть любым натуральным числом. 12. Дано целое число k ( 13. Дано число типа Word. Определить номер самого старшего бита отличного от нуля(Оператор Case должен содержать 16 меток). 14. Решите предыдущую задачу, с условием, что оператор Case должен содержать не более 8 меток. 15. Дана последовательность цифр, представляющая собой записанные подряд ноль и 20 первых натуральных чисел. Найти цифру с номером п в этой последовательности ( 16. Даны целое число k ( 17. Даны целое число k (
|

 при х= 1, у=- 1;
при х= 1, у=- 1; 0) или (
0) или ( 4) при
4) при 
 и
и  при
при  ;
; при
при  и (у > х)при
и (у > х)при  .
. при
при 
 или (
или ( ;
; ) и (
) и ( > 4) при
> 4) при 
 и
и  и (у > х)при
и (у > х)при  ).
). и двузначного
и двузначного  , где
, где 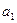 и
и  - число единиц,
- число единиц,  и
и  - число десятков,
- число десятков,  - число сотен. Получить:
- число сотен. Получить: ).Выяснить, имеет ли уравнение
).Выяснить, имеет ли уравнение  вещественные корни.
вещественные корни. п
п  a x > b,
a x > b, , 0 < n
, 0 < n  ). Определить название месяца (январь, февраль и т.п.) этого дня.
). Определить название месяца (январь, февраль и т.п.) этого дня. , если 3<=x<4,
, если 3<=x<4, , если 4<=x<5,
, если 4<=x<5, если 5<=x<6.
если 5<=x<6.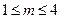 ) определить название соответствующей масти.
) определить название соответствующей масти. ) определить достоинство соответствующей карты.
) определить достоинство соответствующей карты. ). Определить, каким будет k-й день года: выходным (суббота и воскресенье) или рабочим, если 1 января — понедельник.
). Определить, каким будет k-й день года: выходным (суббота и воскресенье) или рабочим, если 1 января — понедельник. ).
). ) и последовательность цифр 505152... 9899100101... 149150, в которой выписаны подряд все натуральные числа от 50 до 150. Определить k -ю цифру.
) и последовательность цифр 505152... 9899100101... 149150, в которой выписаны подряд все натуральные числа от 50 до 150. Определить k -ю цифру. ) и последовательность цифр 123…91011…9899100101…109110, в которой выписаны подряд все натуральные числа от 1 до 110. Определить k -ю цифру.
) и последовательность цифр 123…91011…9899100101…109110, в которой выписаны подряд все натуральные числа от 1 до 110. Определить k -ю цифру.


