Оценки меры изменчивости
31. Выборочная дисперсия – это точечная оценка дисперсии генеральной совокупности. Для несгруппированной выборки формула для нахождения выборочной дисперсии имеет вид:
Здесь n – объем выборки, Для сгруппированной выборки формула для нахождения выборочной дисперсии имеет вид:
Здесь n – объем выборки, k – количество групп выборки, Для интервального ряда в последней формуле вместо
32. Выборочное среднеквадратическое отклонение – это точечная оценка среднеквадратического отклонения генеральной совокупности.
33. Исправленная дисперсия это наилучшая оценка генеральной дисперсии.
34. Исправленной среднеквадратическое отклонение или стандартное отклонение – это наилучшая оценка среднеквадратического отклонения генеральной совокупности.
Исправленная дисперсия и стандартное отклонение являются несмещенными оценками, т. е. оценками, которые не дают систематической ошибки.
35. Эмпирическая функция распределения находится по формуле:
Здесь n – это объем выборки; Эмпирическая функция распределения – ступенчатая. Необходимо разбить ось на интервалы точками
36. Метод наименьших квадратов (МНК) – это метод нахождения точечных оценок неизвестных параметров распределения. Часто он используется для нахождения оценок параметров зависимости между случайными величинами X и Y. Пусть X и Y связаны зависимостью вида
37. Пусть зависимость между X и Y имеет линейный вид, т. е. Чтобы найти оценки неизвестных параметров а и b необходимо: 1. С помощью расчетной таблицы рассчитать коэффициенты системы линейных алгебраических уравнений (СЛАУ). Расчетная таблица
2. Подставить полученные коэффициенты в СЛАУ:
3. Решить СЛАУ любым известным методом. 4. Построить в координатных осях данные точки
38. Уравнение линейной регрессии Y по X имеет вид:
Здесь х – независимая переменная;
Уравнение линейной регрессии можно записать и через выборочный коэффициент корреляции:
Здесь Свойства 1. 2. Если 3. Если 4. Если X и Y независимы, то 5. Если
|

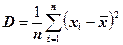 .
.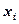 – выборочные значения.
– выборочные значения. .
.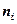 – соответствующие им частоты.
– соответствующие им частоты.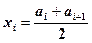 ;
; 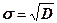 .
. .
.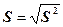 .
. .
. – это накопленная частота числа х, т. е. число выборочных данных, строго меньших х.
– это накопленная частота числа х, т. е. число выборочных данных, строго меньших х. . Пусть даны результаты измерений
. Пусть даны результаты измерений  ,
, 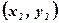 , …,
, …, 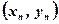 . Чтобы найти неизвестные параметры зависимости вычисляют рассогласования
. Чтобы найти неизвестные параметры зависимости вычисляют рассогласования  , возводят их в квадрат, чтобы исключить их взаимное уничтожение из-за разных знаков, затем складывают. Полученную сумму минимизируют, находя, тем самым, оценки неизвестных параметров зависимости.
, возводят их в квадрат, чтобы исключить их взаимное уничтожение из-за разных знаков, затем складывают. Полученную сумму минимизируют, находя, тем самым, оценки неизвестных параметров зависимости. .
.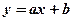 .
.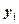
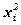
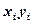
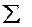
 ;
;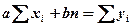 .
.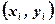 и полученную прямую и убедится в адекватности модели объекту.
и полученную прямую и убедится в адекватности модели объекту. .
.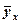 – зависимая переменная (условное среднее значений величины Y, при условии, что Х = х);
– зависимая переменная (условное среднее значений величины Y, при условии, что Х = х); – коэффициент регрессии Y по X;
– коэффициент регрессии Y по X;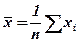 – среднее по х;
– среднее по х; – среднее по у;
– среднее по у;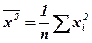 – среднее квадратов;
– среднее квадратов; – среднее произведений.
– среднее произведений.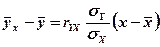 .
. и
и 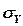 – выборочные среднеквадратические отклонения величин Х и Y.
– выборочные среднеквадратические отклонения величин Х и Y.  – выборочный коэффициент корреляции.
– выборочный коэффициент корреляции. :
: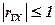 .
. , то связь между X и Y наиболее тесная – линейная.
, то связь между X и Y наиболее тесная – линейная.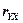 =1, то связь прямая, если
=1, то связь прямая, если 


