Первичная обработка выборки20. Генеральной совокупностью называется множество всех мыслимых измерений некоторой случайной величины. Выборочной совокупностью или выборкой называется некоторой множество значений генеральной совокупности, предназначенное для непосредственного исследования. Количество элементов выборки n – называется объемом выборки. Суть выборочного метода заключается в том, что по выборке делается вывод о генеральной совокупности в целом.
21. Ранжированным рядом называется выборка, упорядоченная по возрастанию.
22. Если выборка сделана из множества значений дискретной случайной величины, то она может быть сгруппирована в дискретный вариационный ряд.
Дискретный вариационный ряд или просто вариационный ряд – это соответствие между вариантами их частотами
или вариантами и их относительными частотами
Варианты Относительная частота варианты
23. Если выборка сделана из множества значений непрерывной случайной величины, то она может быть сгруппирована в интервальный вариационный ряд.
Интервальный вариационный ряд или просто интервальный ряд – это соответствие между частичными интервалами (интервалами группировки) их частотами (или относительными частотами).
Частота интервала
24. Накопленной частотой действительного числа х – называется количество выборочных данных, лежащих левее х на числовой оси. Обозначается –
Накопленной частотой i-ого интервала называется количество выборочных данных, лежащих от начала выборки до конца этого интервала. Обозначается –
25. Полигон частот – это ломаная линия с узлами в точках
По полигону можно найти моду дискретного вариационного ряда.
26. Гистограмма – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы, а высоты соответствуют частоте.
По гистограмме можно найти моду интервального ряда.
27. Кумулята – это ломаная линия, с узлами в точке
По кумуляте можно найти медиану интервального ряда.
|
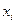
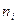
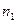
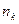
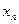
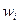
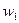
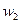
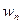
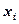- это неповторяющиеся выборочные значения. Частота варианты 
- это число, показывающее, сколько раз варианта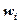 
= 
.
.
.
.
.
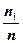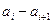
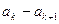
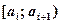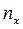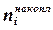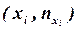для дискретного вариационного ряда и с узлами в точках 
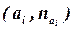для интервального ряда.
