Исследование температурной зависимости удельной теплоемкости веществ
Цель работы: ознакомление с устройством и методами работы на установке ИТ-λ-400, исследование температурной зависимости истинной удельной теплопроводности твердых материалов. 1.1 Теоретические сведения. Теплопроводность представляет собой процесс распространения энергии между частицами тела, находящимися друг с другом в соприкосновении и имеющими различные температуры. Рассмотрим нагрев какого-либо однородного и изотропного тела (в дальнейшем будем рассматривать только такие тела). Изотропным называют тело, обладающее одинаковыми физическими свойствами по всем направлениям. При нагреве такого тела температура его в различных точках изменяется во времени и теплота распространяется от точек с более высокой температурой к точкам с более низкой температурой. Из этого следует, что в общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры t как в пространстве, так и во времени:
(1.1)
где х, у, z—координаты точки; t-время. Эта функция определяет температурное поле в рассматриваемом теле. В математической физике температурным полем называют совокупность значении температуры в данный момент времени для всех точек изучаемого пространства, в котором протекает процесс.
Такое поле отвечает неустановившемуся тепловому режиму теплопроводности.
Уравнения двухмерного температурного поля для режима: стационарного нестационарного На практике встречаются задачи, когда температура тела является функцией одной координаты, тогда уравнения одномерного температурного поля для режима: стационарного нестационарного Одномерной, например, является задача о переносе теплоты в стенке, у которой длину и ширину можно считать бесконечно большими по сравнению с толщиной. Основной закон теплопроводности Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой градиент температуры в различных точках тела не должен быть равен нулю.
Минус в правой части показывает, что в направлении теплового потока температура убывает и grad t является величиной отрицательной. Множитель пропорциональности λ; называют теплопроводностью. Уравнение (1.4) носит название основного уравнения теплопроводности или закона Фурье. Справедливость гипотезы Фурье подтверждается опытами.
где dA — элементарная площадь; п— длина нормали к изотермической поверхности. Вектор плотности теплового потока направлен по нормали к изотермической поверхности в сторону убывания температуры. Векторы q и grad t лежат на одной прямой, но направлены в противоположные стороны.
Количество теплоты, прошедшее через эту поверхность в течение времени τ,
Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности. Теплопроводность λ есть физический параметр вещества, характеризующий его способность проводить теплоту. Теплопроводность можно определить из уравнения (1.8):
где q—поверхностная плотность теплового потока, Вт/м2; дt/дп — температурный градиент, К/м. Единица теплопроводности — Вт/(м-К). Числовое значение теплопроводности определяет количество теплоты, проходящей через единицу изотермической поверхности в единицу времени, при условии, что градиент температуры равен единице (grad t=1). Теплопроводность зависит от давления и температуры. Для большинства веществ теплопроводность определяется опытным путем и для технических расчетов берется из справочных таблиц. Как показывают опыты, для многих материалов зависимость теплопроводности от температуры может быть принята линейной:
где λо—теплопроводность при температуре t0 °С; t—температура, °С; b — температурный коэффициент, определяемый опытным путем. Лучшими проводниками теплоты являются металлы, у которых теплопроводность изменяется от 3 до 458 Вт/(м-К). Теплопроводности чистых металлов, за исключением алюминия, с возрастанием температуры убывают. Теплоту в металлах переносят главным образом свободные электроны. Самым теплопроводным металлом является чистое серебро [Х==458 Вт/(м.К)]. Теплопроводность теплоизоляционных и строительных материалов, имеющих пористую структуру, при повышении температуры возрастает по линейному закону и изменяется в пределах от 0,02 ДО 3,0 Вт/(м.К). Значительное влияние на теплопроводность пористых материалов оказывают газы, заполняющие поры и обладающие весьма малой теплопроводностью по сравнению с теплопроводностью твердых компонентов. Увеличение λ пористых материалов при повышении температуры объясняется значительным возрастанием теплообмена излучением между поверхностями твердого «скелета» пор через разделяющие их воздушные ячейки. Роль конвекции в росте λ возрастает с увеличением размеров воздушных включений в материал. Поэтому эффективная теплопроводность пористых тел имеет сложную природу и является условной величиной, которая имеет смысл теплопроводности некоторого однородного тела; через это тело при одинаковой форме, размерах и температуре на границах проходит то же количество теплоты, что и через данное пористое тело. Большое влияние на λ оказывает влажность вещества. Опыты показывают, что с увеличением влажности материала теплопроводность значительно возрастает. Кроме того, чем выше объемная плотность материала, тем меньше он имеет пор и тем выше его теплопроводность. Теплопроводность большинства капельных жидкостей с повышением температуры убывает; ее значения находятся в пределах от 0,08 до 0,65 Вт/(м-К). Вода является исключением: с увеличением температуры от 0 до 127 °С теплопроводность повышается, а при дальнейшем возрастании температуры уменьшается. От давления λ капельных жидкостей практически не зависит. Теплопроводность газов при повышении температуры возрастает. Опытные исследования показывают, что λ газов изменяется от 0,005 до 0,6 Вт/(м-К). От давления λ газов практически не зависит. Ниже для расчетов приводятся числовые значения теплопроводности и температуропроводности некоторых материалов при различных плотностях, температурах и теплоемкостях 1.2 Приборы и оборудование. Физическая основа и принцип работы измерителя ИТ – λ – 400 Измеритель теплопроводности ИТ-λ-400 (далее измеритель) предназначен для исследования температурной зависимости твердых, механически обрабатываемых материалов в режиме монотонного нагрева. В основу работы измерителя положен метод динамического калориметра с тепломером и адиабатической оболочкой.
Рисунок 1.1 - Измерительная ячейка
1- пластина, 2- пластина контактная, 3- термопара, 4- колпак охранный, 5- коробка из фольги, 6- пружина, 7- пружина, 8- патрубок, 9- корпус, 10- оболочка теплозащитная, 11- стержень, 12- образец испытуемый, 13- основание, 14-блок нагревательный, 15-патрубок. Испытуемый образец 12 помещается на основание 13. Опускается верхняя половина корпуса измерительной ячейки 9. Подается напряжение на основной нагреватель 14, и ядро измерительной ячейки начинает плавно, монотонно разогреваться до верхней, предельной для каждого образца, температуры. Во время разогрева с помощью нагревателя теплозащитной оболочки 10, расположенного в верхней части измерительной ячейки, поддерживаются теплозащитное условия. Для регулирования работы нагревателя используются термопары 3. В эксперименте, в процессе непрерывного разогрева на различных уровнях температуры (через 25 0С), с помощью Ф 195 (далее милливольтметр) и секундомера, измеряется временное запаздывание температуры ампулы по отношению к температуре основания. Блок питания и регулирования обеспечивает нагрев ядра измерительной ячейки с заданной скоростью (около 0,1 К/с) и автоматическое регулирование температуры внутри. Скорость разогрева определяется величиной начального напряжения и скоростью его изменения. Обе эти величины строго фиксированы. 1.3 Порядок выполнения работы Перевести выключатели «СЕТЬ» и «НАГРЕВ» блока питания и регулирования в положение «ВЫКЛ», а ручку регулятора напряжения оттянуть на себя и повернуть до отказа против часовой стрелки. Установить на блоке измерительном переключатель «ИЗМЕРЕНИЕ» в положение «УСТ.0», переключатель «ТЕМПЕРАТУРА» - в положение «25 0С». Установить выключатель «СЕТЬ» милливольтметра в положение «ВЫКЛ», переключатель режима работы, переключатель диапазона – в положение «ImА». Поднять и повернуть на 900 верхнюю часть измерительной ячейки блока измерительного. Протереть контактные поверхности образца. Взвесить образец с точностью Записать начальную (Тнач) и конечную (Ткон) температуру измерений (значения задаются преподавателем). Повернуть на 900 и опустить верхнюю часть измерительной ячейки. Подключить блок питания и регулирования и милливольтметр к сети 220 В. Включить выключатель «СЕТЬ» блока питания и регулирования и выключатель «СЕТЬ» милливольтметра, дать приборам прогреться в течение 5 минут. После прогрева проверить положение нуля милливольтметра: стрелка прибора должна стоять на отметке 50 Установить по вольтметру блока питания и регулирования начальное напряжение 40 Включить кнопкой «НАГРЕВ» блока питания и регулирования основной нагреватель. Перевести переключатель «ИЗМЕРЕНИЕ» блока измерительного в положение «t1», а переключатель «ТЕМПЕРАТУРА» - в положение, соответствующее температуре, при которой измеряется теплоемкость образца (измерения начинать с наименьшей температуры). В момент прохождения стрелки милливольтметра через отметку 50 (по верхней шкале) включить секундомер. Для более точного определения момента прохождения стрелки через отметку 50 следует визуально совместить стрелку и ее отражение на зеркальной части шкалы прибора. Перевести переключатель «ИЗМЕРЕНИЕ» блока измерительного в положение «t2», стрелка милливольтметра при этом должна сместиться влево. В момент прохождения стрелки милливольтметра через отметку 50 (по верхней шкале) выключить секундомер. Записать показания секундомера ( Записать время начала измерений (tнач). Время измерения составляет 10-40 с. Время нагрева образца от одного значения температуры, при котором производится измерение теплопроводности, до следующего (если измерения производятся через 25 0С) от 3 до 5 минут. Повторить измерение времени При достижении заданного максимального значения температуры (Ткон), записать время окончания измерений (tкон). Выключить выключатели «СЕТЬ» и «НАГРЕВ» блока питания и регулирования, выключатель «СЕТЬ» милливольтметра. Отключить блок питания и регулирования и милливольтметр от сети. Поднять и повернуть на 900 верхнюю часть корпуса измерительной ячейки для ее охлаждения. Необходимо помнить, что разогрев измерительной камеры может производиться до температуры плюс 400 0С, поэтому после опыта недопустимо прикосновение к внутренним частям измерительной ячейки. Смену исследуемого образца производить только после охлаждения измерительной ячейки до комнатной температуры. При проведении измерений следует обращать внимание на работу регулятора температуры адиабатической оболочки и механизма регулирования напряжения. При нормальной работе регулятора он должен периодически включаться и выключаться с периодом 10-60 с, о чем сигнализирует индикатор «РАБОТА РЕГУЛЯТОРА», расположенный на блоке измерительном. Напряжение на нагревательных элементах основного нагревателя и нагревателя адиабатической оболочки должно повышаться на 40-80 В/час при включенном выключателе «НАГРЕВ», что можно проконтролировать по вольтметру блока питания и регулирования и по уровню свечения индикатора «РАБОТА РЕГУЛЯТОРА». Результаты измерений заносятся в таблицу 1.1 и таблицу 1.2. Обработка результатов измерений
Вычислить и занести в таблицу 3 среднее значение времени запаздывания температуры на тепломере
где Вычислить и занести в таблицу 3 доверительный интервал значений
+ (
где tp5 = 2,78 – коэффициент Стьюдента (для 5 опытов и вероятности 0,95). Определить промахи при проведении измерений, для чего вычислить и занести в таблицу 3 величину относительного отклонения величины Е где Е Измерение считать промахом, если его отклонение от среднего превышает 20 %. В случае, если измерение окажется промахом, из дальнейших расчетов его не исключать.
Таблица 1.1 Полученные данные
Вычислить и занести в таблицу 1.2 величину относительной погрешности среднего времени запаздывания температуры на тепломере для каждого значения температуры по формуле: Е где Е Вычислить и занести в таблицу 1.3 удельную теплоемкость образца для каждого значения температуры по формуле:
СТ = KT (
где СТ, Дж/ (кг К) – удельная теплоемкость образца при температуре Т; КТ, Вт / К – тепловая проводимость тепломера при температуре Т;
Таблица 1.2 Расчетные данные
Вычислить и занести в таблицу 3 величину относительной погрешности удельной теплоемкости образца для каждого значения температуры по формуле:
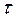 срТ срТ  срТ / ( срТ / (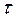 срТ - срТ - 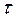 0срТ ))2 + 0срТ ))2 +
+ (E где ЕсТ , % - относительная погрешность удельной теплоемкости образца; ЕКТ, % - относительная погрешность тепловой проводимости тепломера; E
b = (Tкон - Тнач) / (tкон - tнач ), где b, K / c – средняя скорость разогрева; Тнач,
сср где сср, дж / кг К – средняя удельная теплопроводность образца: R = 8314 Дж / кмоль К – универсальная газовая постоянная;
сminT = cT (1 - EcT / 100) построить совмещенный график функций: сТ = F(T); сmaxT = F(T); сminT = F(T).
1.4 Содержание отчета о работе Отчет о работе должен содержать: наименование и цель работы, краткое описание методики экспериментального определения удельной теплоемкости, тепловую схему метода, таблицы результатов измерений и расчетов (таблицы 1,2,3), расчеты, график. Контрольные вопросы 1. Что называется теплопроводностью? 2. Дать определение теплового потока. 3. Влияние температуры на теплопроводность веществ?
|



 . (1.2)
. (1.2)
 . (1.3)
. (1.3)
 ,
, .
.
 ,
,
 .
. ,
, . (1.6)
. (1.6) .
. ,
, ,
,
 0,01 г установить образец, прижать его к нижней контактной поверхности пластины, закрыть крышку.
0,01 г установить образец, прижать его к нижней контактной поверхности пластины, закрыть крышку. т).
т). срТ, в опытах с образцом для каждого значения температуры по формуле:
срТ, в опытах с образцом для каждого значения температуры по формуле:
 Т, с
Т, с


 0срТ) / m0,
0срТ) / m0, С
С
 С – начальная температура; Ткон,
С – начальная температура; Ткон,  3R/
3R/  ,
, , кг / моль – относительная молекулярная масса вещества образца.
, кг / моль – относительная молекулярная масса вещества образца.


