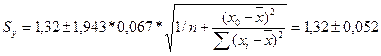Решение. Поле рассеяния характеризует зависимость потребительских расходов от денежных доходов

Поле рассеяния характеризует зависимость потребительских расходов от денежных доходов. Очевидно, между ними существует прямая зависимость.

Визуальный анализ поля рассеяния позволяет выдвинуть гипотезу о линейной зависимости потребительских расходов от денежных доходов и записать эту зависимость в виде линейной модели:

y = a₀ + a₁x + e

где y - результативный фактор (потребительские расходы)

a₀ a₁ - параметры модели (постоянные)

е - некоторая изменяющаяся величина, благодаря которой любое индивидуальное значение y может отклоняться от линии регрессии.

Оценим параметры регрессии. Для удобства вычисления оценок искомых коэффициентов модели составим таблицу.

№ субъекта РФ	x	y	x2	xy	y2	yi	yi-yi	(yi-yi)2
	1,66	1,08	2,7556	1,7928	1,1664	1,135	-0,055	0,003019
	1,75	0,82	3,0625	1,435	0,6724	1,194	-0,374	0,139652
	1,59	1,04	2,5281	1,6536	1,0816	1,089	-0,049	0,002426
	1,58	1,34	2,4964	2,1172	1,7956	1,083	0,257	0,066191
	2,36	1,72	5,5696	4,0592	2,9584	1,592	0,128	0,016408
	2,35	1,55	5,5225	3,6425	2,4025	1,585	-0,035	0,001252
	1,44	0,89	2,0736	1,2816	0,7921	0,991	-0,101	0,010268
	1,5	1,26	2,25	1,89	1,5876	1,031	0,230	0,05267
сумма	14,23	9,7	26,2583	17,8719	12,4566			0,291885

 

Следовательно,

x = åx_i / 8 = 14,23 / 8 = 1,78 тыс. руб. – среднее значение среднедушевых доходов

`y = åy_i / 8 = 9.7 / 8 = 1,21 тыс. руб. – среднее значение среднедушевых потребительских расходов.

xy = 17.87 / 8 = 2.23

`x² = 26,26 / 8 = 3.28

Тогда,

a₁ = 0,077 / 0,118 = 0,65

a₀ = `y - a<sub>1</sub> *`x = 0,051

Таким образом, искомое уравнение регрессии имеет вид:

y = 0,051 + 0,65*x

Выборочный коэффициент парной корреляции:

r_xy = 0,762

Для того, чтобы с большей уверенностью полагаться на значение коэффициента корреляции выясним значимо ли значение коэффициента корреляции.

Рассчитаем статистику:

При уровне значимости а = 0,1, t (0,95; 6) = 1,943

Так как |t| < t_табл, то коэффициент корреляции не существенно отличается от нуля и существует слабая связь между x и y.

Коэффициент детерминации определяется по формуле:

R² = å(y’_i -`y)<sup>2</sup> / å(y<sub>i</sub> -`y)² = 1 – (å(y_i – y’_i)² / å(y_i -`y)²)

å(y_i – y’_i)² - это мера разброса, объясненная с помощью уравнения регрессии;

å(y_i -`y)² - это мера разброса не объясненная уравнением регрессии.

R² = 1-0.292/ 0,695=0.58

Уравнение регрессии достаточно точно отражает истинную зависимость между доходами и расходами.

4. Найдем точечный прогноз для 8-го субъекта.

x₀ = 1,3* 1,5 = 1,95 тыс. руб.

y’₀ = a + b*x₀ = 1,32 тыс. руб.

Интервальным прогнозом зависимой переменной y, соответствующим некоторому значению переменной x = x₀, называется доверительный интервал, границы которого находятся по формуле:

y_вн = y(x₀) ± t_{1-a/2, n-2} Sy

где y(x₀) - точечный прогноз

Пусть a = 0,1, тогда 1 - a = 0,9; t_{1-a/2, n-2} = 1,943

S² = å(y’_i -`y_i)² / (n-2)=0,067;

å(x₁ –`x)<sup>2</sup> = åx<sub>i</sub><sup>2</sup> – n * (`x)² =0,95

Тогда

Следовательно, y’_в,н = y’(x₀) ± t_{1-a/2, n-2} * Sy_i = 1.32 ± 0,052

y’_в = 1,372 y’_н = 1,268

 

Это означает, что при увеличении среднедушевых денежных доходов в на 30%, размер среднедушевых среднемесячных потребительских расходов с вероятностью 0,9 будет колебаться в пределах от 1,268 тыс. руб. до 1,372 тыс. руб.

Следовательно, y₀ Î (1,268; 1,372) с 90% вероятностью.

Рассмотрим найденное уравнение регрессии y = 0,051+ 0,653*x. Оно было найдено по методу наименьших квадратов. Прямая регрессии, изображенная на рисунке поля рассеяния наилучшим образом приближается к заданным точкам, т.к. сумма квадратов отклонений фактических значений y от расчетных минимально.

Коэффициент а₀ = 0,051 не имеет экономического смысла, поскольку формально соответствует размеру потребительских расходов при нулевом уровне денежных доходов. Коэффициент а₁ = 0,653 определяет прирост потребительских расходов, обусловленный приростом денежных доходов, т.е. прирост денежных доходов, например, на 100 руб. вызовет прирост потребительских расходов на 65,3 руб.

Выпишем итоговые результаты.

y = а0 + а1 * x + е	- математическая модель зависимости потребительских расходов от денежных доходов
y’ = 0,051+ 0,653 * x	- уравнение регрессии, количественно выражающее зависимость расходов от доходов
rxy = 0.762	- коэффициент корреляции между x и y, его значение свидетельствует о наличии тесной линейной зависимости между доходами и расходами
R2 = 0,58	- коэффициент детерминации, его значение показывает, что уравнение регрессии отражает имеющуюся зависимость между расходами и доходами
y’0 = 1,32	- точечный прогноз. Так как вероятность совпадения фактических потребительских расходов (вероятность попадания в любую точку) равна нулю, то были составлены интервальные прогнозы
y’н = 1,268; y’в = 1.372	- интервальный прогноз с 90%-ой доверительной вероятностью