Задача №11
Учитывая движение ядра атома водорода и боровское условие квантования, найти: 1) возможные расстояния между электроном и ядром; 2) возможные значения полной кинетической энергии; 3) энергию связи электрона; 4) на сколько процентов отличается энергия связи и постоянная Ридберга, полученные без учета движения ядра, от соответствующих уточненных значений этих величин. Пусть R и r – расстояния, соответственно от ядра и электрона до общего центра вращения. Тогда согласно 2-му Закону Ньютона
Согласно правилу квантования Бора
где L – момент импульса, равный в данном случае,
тогда
Используя связь линейной и угловой скорости
перепишем (17) в следующем виде
или
Подставляя, полученные выражения в (18), получим
Отсюда
Подставив найденное выражение для w в (19) найдем выражения для R и r
Отсюда
где Полная кинетическая энергия атома водорода в данном случае будет складываться из кинетической энергии вращательного движения ядра КЯ и электрона Ке
Подставляя сюда выражение, найденное выше для а, получим
Полная энергия системы равна сумме кинетической и потенциальной энергий
Тогда выражение для энергии связи (n = 1) будет иметь следующий вид:
где Сравнивая полученные выражения для постоянной Ридберга R и энергии связи Есв с аналогичными выражениями, полученными нами ранее, но без учета движения ядра (т.е M = ¥), можно видеть, что
Подставляя численные значения, оказывается, что разница составляет 0,055%. Несмотря на столь малое различие, его удается зафиксировать с помощью современных спектральных приборов.
|


 , (17)
, (17) , М и m – массы ядра и электрона, соответственно, vЯ и vе – их скорости, а – расстояние между ядром и электроном, равное R + r.
, М и m – массы ядра и электрона, соответственно, vЯ и vе – их скорости, а – расстояние между ядром и электроном, равное R + r. , где n = 1,2,3…,
, где n = 1,2,3…, ,
, . (18)
. (18)
 ,
,
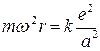 (19)
(19)

 .
. .
. ,
,  .
. ,
, – приведенная масса.
– приведенная масса. .
. .
. .
. ,
, – уточненное выражение для постоянной Ридберга.
– уточненное выражение для постоянной Ридберга.
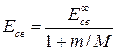 .
.


