Логические основы компьютера
Дискретный преобразователь, который после обработки входных двоичных сигналов выдаёт на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом. Ниже приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).
Рис. 3.1. Конъюнктор, дизъюнктор и инвертор
Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов. Пример 3.13. По заданной логической функции F(A, B) = B & Построение необходимо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Пример 3.14. Логическая схема имеет два входа X и Y. Определить логические функции F1(X,Y) и F2(X,Y), которые реализуются на ее двух выходах.
Функция F1(X,Y) реализуется на выходе первого конъюнктора, т.е. F1(X,Y) = X & Y. Одновременно сигнал с конъюнктора подается на вход инвертора, на выходе которого реализуется сигнал На другой вход второго конъюнктора подается сигнал X Ú Y с дизъюнктора, следовательно, функция F2(X,Y) =
Рассмотрим схему сложения двух n-разрядных двоичных чисел. При сложении цифр i-го разряда складываются аi и bi, а также pi-1 — перенос из i-1разряда. Результатом будет si – сумма и pi — перенос в старший разряд. Таким образом, одноразрядный двоичный сумматор — это устройство с тремя входами и двумя выходами. Пример 3.15. Построить таблицу истинности одноразрядного двоичного сумматора, воспользовавшись таблицей сложения двоичных чисел.
Триггер. Для хранения информации в оперативной памяти компьютера, а также во внутренних регистрах процессора используются триггеры. Триггер может находиться а одном из двух устойчивых состояний, что позволяет запоминать, хранить и считывать 1 бит информации. Самый простой триггер — RS-триггер. Он состоит из двух элементов ИЛИ-НЕ (смотри задание 3.34), входы и выходы которых соединены кольцом: выход первого соединен со входом второго и выход второго – со входом первого. Триггер имеет два входа S (от англ. set – установка) и R (от англ. reset – сброс) и два выхода Q (прямой) и
Рис. 3.2. Логическая схема RS-триггера Пример 3.16. Построить таблицу истинности для RS-триггера. Если на входы поступают сигналы R = 0 и S = 0, то триггер находится в режиме хранения, на выходах Q и Если на установочный вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет сохранять это состояние, т.е. будет хранить 1. При подаче 1 на вход R триггер перейдет в состояние 0. Подача на оба входа S и R логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.
|



 Ú
Ú  & A построить логическую схему.
& A построить логическую схему.
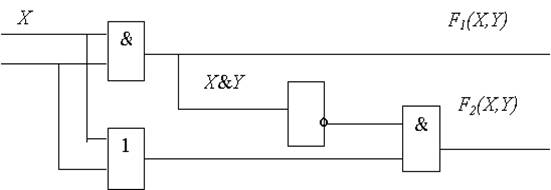
 , который, в свою очередь, подается на один из входов второго конъюнктора.
, который, в свою очередь, подается на один из входов второго конъюнктора. (инверсный).
(инверсный).



