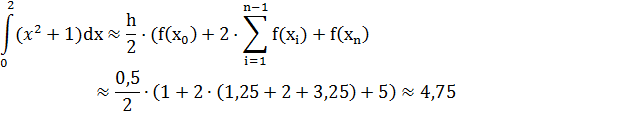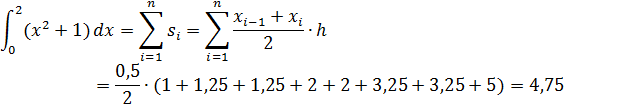СЕМІНАРСЬКІ ЗАНЯТТЯ
З КУРСУ
ПОРІВНЯЛЬНОЇ ПЕДАГОГІКИ
Укладачем використано матеріали навчального видання:
Курс лекцій з порівняльної педагогіки за загальною редакцією професора
Г. В. Троцко. – Харків, 2007. – 264 с.
II. Application Documents
| Chinese Government Scholarships
| Zhejiang Provincial Government Scholarships
| ZSTU IntЎЇl Student Scholarships
|
| 1. ZSTU International Students Application Form
| 1. ZSTU International Students Application Form
| 1. ZSTU International Students Application Form
|
| 2. Application Form for Chinese Government Scholarships
| 2. Application Form for Zhejiang Provincial Government Scholarships
| 2. Application Form for ZSTU IntЎЇl Student Scholarships
|
| 3. Copy of valid passport
| 3. Copy of valid passport
| 3. Copy of valid passport
|
| 4. Highest diploma (notarized photocopy). Documents in languages other than Chinese or English must be attached with translations in Chinese or English.
| 4. Highest diploma (notarized photocopy). Documents in languages other than Chinese or English must be attached with translations in Chinese or English.
| 4. Highest diploma (notarized photocopy). Documents in languages other than Chinese or English must be attached with translations in Chinese or English.
|
| 5. Notarized copy of transcripts. Transcripts in languages other than Chinese or English must be attached with translations in Chinese or English.
| 5. Notarized copy of transcripts. Transcripts in languages other than Chinese or English must be attached with translations in Chinese or English.
| 5. Notarized copy of transcripts. Transcripts in languages other than Chinese or English must be attached with translations in Chinese or English.
|
| 6. Applicants overseas for master or doctoral degree studies and senior scholars must submit two letters of recommendation in Chinese or English by professors or associate professors.
| 6. Applicants for master or doctoral degree studies and senior scholars must submit two letters of recommendation in Chinese or English by professors or associate professors.
| 6. Applicants for master or doctoral degree studies and senior scholars must submit two letters of recommendation in Chinese or English by professors or associate professors.
|
| 7. Foreigner Physical Examination Form (the report is valid for 6 months)
| 7. Foreigner Physical Examination Form (the report is valid for 6 months)
| 7. Foreigner Physical Examination Form (the report is valid for 6 months)
|
| 8. Applicants under the age of 18 should submit the legal documents of their legal guardians in China.
| 8. Applicants under the age of 18 shall submit the legal documents of their legal guardians in China.
| 8. Applicants under the age of 18 should submit the legal documents of their legal guardians in China.
|
| 9. Applicants for fine arts must submit six color photographs of personal works (two sketches, two color paintings and two other works).
| 9. Valid copy of Chinese Proficiency Test (HSK) at required level
| 9. Valid copy of Chinese Proficiency Test (HSK) at required level
|
| 10. A study or research plan in Chinese or in English
|
|
|
Note: Other documents shall be submitted at request.
Forms can be downloaded in http://admission.zstu.edu.cn/en/news.asp?id=3&type1=7
МЕТОД РЕШЕНИЯ
Метод трапеций
По условию задачи исходными данными являются пределы интегрирования: a – нижний предел, b – верхний предел; также дано количество интервалов разбиения n.
Допустим, наша подынтегральная функция y = f(x) непрерывна на отрезке [a;b], тогда разобьем отрезок [a;b] на количество интервалов n длины h точками, находящимися внутри отрезка (такие точки также называются узлами), то есть a = x0<x1<x2<…<xn1<xn= b. В таком случае шаг разбиения находится как
h =  , ,
| (1.1)
|
узлы определяются из равенства
где xi –i-ый узел;
i = 0, 1, 2,…, n – номер узла.
Теперь рассмотрим подынтегральную функцию на элементарных отрезках [xi-1;xi], где i = 1, 2,…, n (Рис 1.1).
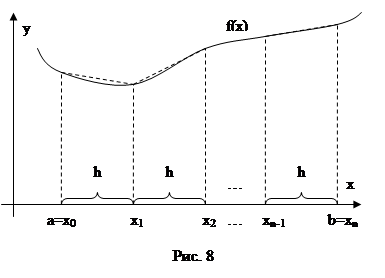
Рисунок 1.1 Метод трапеций
На каждом отрезке [xi-1;xi], i = 1, 2,…, n заменим функцию y = f(x) отрезком прямой проходящей через точки с координатами (xi-1;f(xi-1)) и (xi;f(xi)). В качестве приближенного значения интеграла  возьмем выражение
возьмем выражение  , то есть
, то есть

| (1.3)
|
Мы знаем, что площадь трапеции находится как произведение полу суммы оснований на высоту. Следовательно на рис.1.1, площадь криволинейной трапеции приближенно равна площади трапеции с основаниями f(xi-1), f(xi) и высотой h.
Теперь воспользуемся одним из свойств определенного интеграла, которое гласит, что если функция y = f(x) интегрируема на интервале X, причем a, b, c принадлежит X, то интеграл по всему отрезку равен сумме интегралов по частям этого отрезка
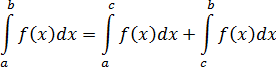
|
(1.4)
|
Тогда по свойству определенного интеграла, если в формулу 1.3 подставить приближенные значения интегралов, получаем

| (1.5)
|
или

| (1.6)
|
В результате мы получаем формулу трапеции для определенного интеграла, которая принимает вид

| (1.7)
|
Проверим полученную формулу на примере, решив задачу аналитическим и графическим способом.
Пример

 – формула трапеции
– формула трапеции
Для нахождения длины интервала разбиения используем формулу 1.1
h = (b-a)/n = 2/4 =0,5
Далее находим координаты всех узлов по формуле 1.2, и значение функции в этих узлах.
| xi = a+i·h;
| f(x) = x2+1;
|
| i=0: x0 = 0+0·0,5 = 0;
| f(x0) = f(0) = 0+1 = 1;
|
| i=1: x1 = 0+1·0,5 = 0,5;
| f(x1) = f(0,5) = 0,25+1 = 1,25;
|
| i=2: x2 = 0+2·0,5 = 1;
| f(x2) = f(1) = 1+1 = 2;
|
| i=3: x3 = 0+3·0,5 = 1,5;
| f(x3) = f(1,5) = 2,25+1 = 3,25;
|
| i=4: x4 = 0+4·0,5 = 2.
| f(x4) = f(2) = 4+1 = 5.
|
Аналитический способ.
Высчитываем определенный интеграл по формуле 1.7
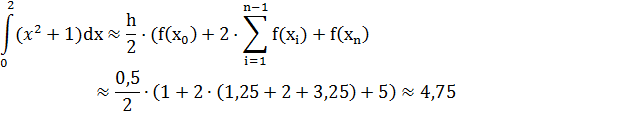
Графический способ
Для решения задачи графическим способом прежде всего нам необходим график. Для построения графика установим зависимость координат x от y на отрезке от [0;2] и узла от значения функции в узле в виде таблиц.
| i
|
|
|
|
|
|
| xi
|
| 0,5
|
| 1,5
|
|
| f(xi)
|
| 1,25
|
| 3,25
|
|
Выберем произвольный масштаб графика, построим оси, отметим полученные точки и соединим их, после разобьем график на элементарные отрезки, соединив ближайшие точки.
| f(x1) f(x2) f(x3) f(x4) f(x5)
f(xi)
f(xi)
f(xi)
|

Рис 1.2 Пример метода трапеций
Мы получили множество трапеций. Теперь осталось лишь посчитать их площади и сложить.
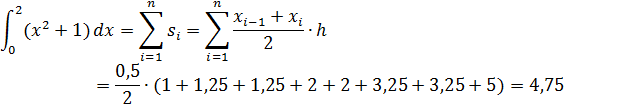
Ответ при графическом и аналитическом решении совпал. Следовательно метод верный.


 ,
,
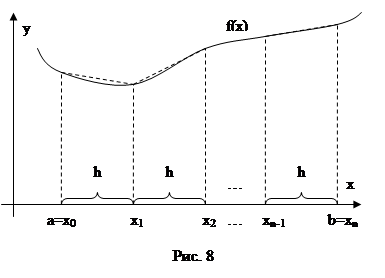
 возьмем выражение
возьмем выражение  , то есть
, то есть
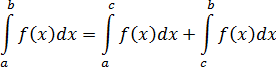




 – формула трапеции
– формула трапеции