Основы термодинамики
● Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекулы,
● Средняя энергия молекулы
где
● Внутренняя энергия газа
где
● Первое начало термодинамики
где Q – количество теплоты, сообщенное системе или отданное ею;
● Первое начало термодинамики для малого изменения системы
● Молярные теплоемкости газа при постоянном объеме и постоянном давлении
● Уравнение Майера
● Изменение внутренней энергии идеального газа
● Работа, совершаемая газом при изменении его объема,
● Полная работа при изменении объема газа
где V1 и V2 – соответственно начальный и конечный объемы газа.
● Работа газа:
при изобарном процессе
при изотермическом процессе
● Уравнение адиабатического процесса (уравнение Пуассона)
где
● Работа в случае адиабатического процесса
где T1 , T2 и V1,V2 – соответственно начальные и конечные температура и объем газа.
● Термический коэффициент полезного действия для кругового процесса (цикла)
где Q1 – количество теплоты, полученное системой; Q2 – количество теплоты, отданное системой; А – работа, совершаемая за цикл.
● Термический коэффициент полезного действия цикла Карно
где T1 – температура нагревателя; T2 – температура холодильника.
● Изменение энтропии при равновесном переходе из состояния 1 в состояние 2, в переменных РV
В переменных Т, V
Примеры решения задач
Задача 1. В баллоне объёмом 20 л находится аргон под давлением 1,0 МПа и температуре 300 К. После того как из баллона было взято20 г аргона, температура в баллоне понизилась до 280 К. Определить давление газа, оставшегося в баллоне.
Решение: Для решения задачи воспользуемся уравнением состояния идеального газа, применив его к начальному и конечному состояниям газа:
Из уравнений (1) и (2) выразим m1 и m2 и найдём их разность:
откуда находим
Проверку решения проведем по размерности физических величин. В правую часть вместо символов величин подставим их единицы измерения. В правой части два слагаемых. Первое из них имеет размерность давления, так как состоит из двух множителей, первый из которых – давление, а второй – безразмерный. Проверим второе слагаемое:
Вычисления произведём по формуле (3) с учётом, что для аргона
Ответ: Р = 875 кПа Задача 2. Определите наиболее вероятную скорость молекул газа, плотность которого при давлении р =40 кПа составляет r =0,35 кг/м3.
Решение: Воспользуемся формулой
Из уравнения состояния выражаем плотность газа:
Тогда, подставляя, получим
Задача 3. Плотность газа увеличили в k 1=3 раза, а температуру уменьшили в k 2=4 раза. Как изменилось число столкновений молекул в единицу времени?
Решение: Среднее число столкновений молекул в единицу времени находится по формуле
где
Формула для вычисления средней скорости:
связь концентрации молекул с плотностью газа определяется формулой:
Эффективный диаметр молекул d, т.е. минимальное расстояние, на которое сближаются при столкновении центры молекул, зависит от скорости сталкивающихся молекул, т.е. от температуры газа (несколько увеличивается при понижении температуры). Но при решении данной задачи это изменение величины d учитывать не будем.
Подставляем записанные выражения в первую формулу:
тогда после изменения давления и температуры
т.е. длина свободного пробега при этом увеличится в
Следует отметить, что в формулы входит именно термодинамическая температура.
Задача 4. Коэффициенты диффузии и внутреннего трения водорода при некоторых условиях равны соответственно D = 1,42 см2/сек и η = 8,5·10-6 Н·сек/м2. Найти число молекул водорода в 1 м3 при этих условиях. Решение: Для решения задачи воспользуемся формулами расчета коэффициента внутреннего трения (динамической вязкости) и коэффициента диффузии:
Объединив формулы (1) и (2), получим
Откуда следует, что плотность водорода равна
С другой стороны плотность газа может быть найдена по формуле
Объединив формулы (3) и (4), получим выражение для массы водорода
Известно, что число молекул
где
Из формул (5) и (6) находим концентрацию молекул газа
Подставим численные значения
Ответ:
Задача 5. Работа расширения некоторого двухатомного идеального газа составляет А =2 кДж. Определите количество подведенной к газу теплоты, если процесс протекал: 1) изотермически; 2) изобарно; Решение: Согласно первому началу термодинамики подведенное к газу количество теплоты Q расходуется им на изменение внутренней энергии и на совершение работы расширения: Q= D U+A. 1) В случае T= const, 2) При p= constполучаем
где D T – изменение температуры при изобарном увеличении объема на D V. Из уравнений начального и конечного состояний получаем:
т.е.
Тогда
где i =5, т.к. газ двухатомный.
Задача 6. Баллон содержит
Решение:
По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева-Клапейрона парциальные давления
Следовательно, по закону Дальтона давление смеси двух газов:
откуда объем баллона
Произведем вычисления, учитывая, что
Ответ:
Задача 7. Гелий массой
Решение:
Определим количество вещества
где – молярная масса гелия.
Рассмотрим каждый участок цикла отдельно.
(1-2):запишем первый закон термодинамики
Работа
где Воспользуемся уравнением состояния идеального газа
где для одноатомного гелия число степеней свободы Тогда Так как
(2-3): Так как
где
(3-1):
где Так как Итого:
Замечание: используя геометрический смысл работы в координатной плоскости (р, V) видно, что работу за цикл можно рассчитать, определив площадь фигуры цикла (в нашем случае – это площадь треугольника).
Ответ:
Задача 8. Двигатель работает как машина Карно и за цикл получает от нагревателя 1. совершаемую за цикл работу; 2. количество теплоты, отдаваемое холодильнику.
Решение:
Запишем формулу для КПД тепловой машины:
т.к. двигатель работает по циклу Карно, то Совершаемая газом работа за цикл где
Количество теплоты
Ответ:
Задача 9. Один моль идеального двухатомного газа, находящегося в закрытом сосуде, охладили с
Решение:
Запишем второй закон термодинамики в формулировке Клаузиуса
где dS – приращение энтропии. По первому закону термодинамики, записанному для элементарного теплового процесса
Элементарное приращение внутренней энергии газа
Для идеального газа молярная теплоемкость при постоянном объеме где i – число степеней свободы. Из уравнения состояния идеального газа следует, что
После деления на абсолютную температуру Т, имеем
Проинтегрируем полученное дифференциальное уравнение, расставляя пределы интегрирования
Итого, приращение энтропии Замечание: Используя полученное выражение для
где Рассчитаем изменение энтропии газа, учитывая, что при закрытом сосуде
Ответ: энтропия газа уменьшилась на
Задача 10. Во сколько раз следует изотермически увеличить объем идеального газа в количестве 3 моль, чтобы его энтропия увеличилась на 25 Дж/К? Решение: Для обратимого процесса
Так как процесс изотермический, то для идеального газа
Изменение энтропии
Из последнего соотношения находим
Показатель экспоненты – величина безразмерная. Вычисления: Ответ:
|

 .
.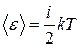 ,
, - число степеней свободы.
- число степеней свободы. ,
,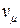 – количества вещества; m – масса газа; μ – молярная масса газа.
– количества вещества; m – масса газа; μ – молярная масса газа. ,
, - изменение её внутренней энергии; А – работа системы против внешних сил.
- изменение её внутренней энергии; А – работа системы против внешних сил. .
. ,
,  .
. .
. .
.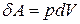 .
. ,
, , или
, или 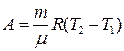 ;
;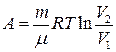 , или
, или  .
.
 - показатель адиабаты.
- показатель адиабаты.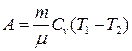 или
или  ,
,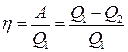 ,
, ,
, .
.
 .
.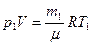 , (1)
, (1) (2)
(2) ,
,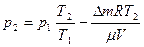 (3)
(3)
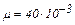 кг/моль.
кг/моль.
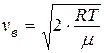 .
. ,
, = 478 м/с.
= 478 м/с.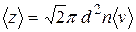 ,
, - средняя скорость движения молекул, d – эффективный диаметр молекул, n – концентрация молекул.
- средняя скорость движения молекул, d – эффективный диаметр молекул, n – концентрация молекул.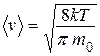 ,
,
 ,
, ,
, =
=  = 1,5 раза.
= 1,5 раза. (1)
(1) (2)
(2)
 (3)
(3) (4)
(4) (5)
(5) можно рассчитать по формуле
можно рассчитать по формуле , (6)
, (6) (молярная масса водорода),
(молярная масса водорода), (число Авогадро).
(число Авогадро).

 = 0, D U
= 0, D U  = 0 и Q 1 = A = 2 кДж.
= 0 и Q 1 = A = 2 кДж. ,
, ,
,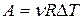 .
. =
=  = 7 кДж.
= 7 кДж. кислорода и
кислорода и  аргона. Давление смеси газов
аргона. Давление смеси газов  , температура
, температура  . Принимая данные газы за идеальные, определить объем V баллона.
. Принимая данные газы за идеальные, определить объем V баллона. кислорода и
кислорода и  аргона выражаются формулами:
аргона выражаются формулами:




 – молярная масса кислорода,
– молярная масса кислорода,  – молярная масса аргона
– молярная масса аргона .
. .
. совершает цикл, изображенный на рисунке. Найти работу А, совершаемую газом за один цикл, количество теплоты, принятое от нагревателя
совершает цикл, изображенный на рисунке. Найти работу А, совершаемую газом за один цикл, количество теплоты, принятое от нагревателя  и переданное холодильнику
и переданное холодильнику  за цикл, КПД цикла, если
за цикл, КПД цикла, если  ,
,  ,
,  ,
,  .
.
 ,
, . На данном участке давление пропорционально объему:
. На данном участке давление пропорционально объему:  , где
, где  .
. определяется, исходя из изотермического смысла работы газа в координатной плоскости (р, V):
определяется, исходя из изотермического смысла работы газа в координатной плоскости (р, V):
 .
. ,
, - молярная теплоемкость при постоянном объеме.
- молярная теплоемкость при постоянном объеме. , тогда
, тогда ,
, .
. .
. , то газ на этом участке получает от нагревателя теплоту.
, то газ на этом участке получает от нагревателя теплоту. , то
, то  и первый закон термодинамики принимает вид
и первый закон термодинамики принимает вид ,
, ;
;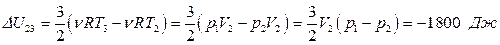 .
. , значит внутренняя энергия уменьшается.
, значит внутренняя энергия уменьшается. . Так как
. Так как  , то газ на этом участке отдает теплоту холодильнику.
, то газ на этом участке отдает теплоту холодильнику. ,
, 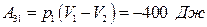 (газ совершает «отрицательную» работу; его сжимают).
(газ совершает «отрицательную» работу; его сжимают).
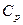 - молярная теплоемкость при постоянном давлении.
- молярная теплоемкость при постоянном давлении. , то газ на участке 3-1 также отдает теплоту холодильнику.
, то газ на участке 3-1 также отдает теплоту холодильнику. ,
, .
. или
или  .
.
 ,
, 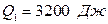 ,
,  ,
,  .
. теплоты. Температура нагревателя
теплоты. Температура нагревателя  , температура холодильника
, температура холодильника  . Найти:
. Найти: ,
, .
. . Тогда
. Тогда  ,
,  ,
, ,
,  .
. (Дж)
(Дж) (Дж).
(Дж). Дж.
Дж. до
до  . На сколько и как изменилась энтропия газа?
. На сколько и как изменилась энтропия газа?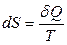 ,
, или
или  .
. , тогда
, тогда .
. ,
, . Тогда
. Тогда .
. ,
, .
.
 ,
, .
. .
. и уравнение Менделеева-Клапейрона для начального и конечного состояний идеального газа, легко получить
и уравнение Менделеева-Клапейрона для начального и конечного состояний идеального газа, легко получить ,
, .
. .
. ,
,  ,
,  (для двухатомного газа число степеней свободы
(для двухатомного газа число степеней свободы 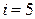 )
) .
. .
.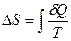 , где
, где .
.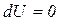 , а элементарная работа равна
, а элементарная работа равна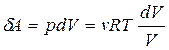 .
. для изотермического процесса будет равно
для изотермического процесса будет равно .
. .
. .
. .
.


