Указания
Последовательность расчета рассмотрим на примере. Пусть 1. Определим расстояние от геометрических осей цилиндра до плоскости постоянного (нулевого) потенциала и расстояние от электрических осей до этой плоскости (рис.2.2).
Расстояние между электрическими и геометрическими осями цилиндров
2. Построим линии равного потенциала
Потенциал произвольной точки М определяется:
Линии равного потенциала являются окружностями. Радиус и абсцисса центра
Определяем значения параметра
Для первой линии:
Для
Для того, чтобы при переходе от одной линии равного потенциала к другой, потенциал увеличивался на одну и ту же величину, необходимо, чтобы число
Следовательно,
Тогда числа
Определяем радиусы и абсциссы центров эквипотенциальных окружностей:
Аналогично определяем:
3. Построим линии напряженности электрического поля. Силовые линии являются дугами окружности
Координаты центров окружностей равны:
Радиусы окружностей:
Напряжение между цилиндрами (разность потенциалов):
Определим расстояния
Учитывая, что
имеем
По этому выражению рассчитываются значения потенциала и строится кривая распределения потенциала по оси 4. Построим кривую распределения напряженности поля по оси
По этому выражению рассчитываются значения модуля вектор напряженности электрического поля и строится кривая распределения напряженности по оси
|

 ,
,  ,
, 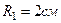 ,
,  .
. ,
,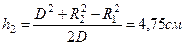 ,
,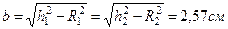 .
. ;
;  .
.
 .
. - ой эквипотенциальной окружности определяются:
- ой эквипотенциальной окружности определяются: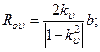
 .
. , соответствующие линиям равного потенциала. Всего линий равного потенциала
, соответствующие линиям равного потенциала. Всего линий равного потенциала 
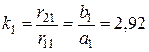 .
. линии:
линии: .
. изменялось в геометрической прогрессии, а именно:
изменялось в геометрической прогрессии, а именно: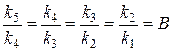 .
. .
. ;
;  ;
;  ;
;  .
.



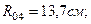
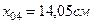 .
. . Первой линией напряженности является линия, для которой угол
. Первой линией напряженности является линия, для которой угол  . Следующие линии проводят через одно и тоже приращение угла
. Следующие линии проводят через одно и тоже приращение угла 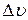 . Для данного примера
. Для данного примера .
. ;
;  .
.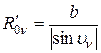 .
. .
. :
:




 .
.
 .
.



