Указания. В зависимости от варианта задачи уравнение Пуассона следует записать в декартовой или цилиндрической системе координат.В зависимости от варианта задачи уравнение Пуассона следует записать в декартовой или цилиндрической системе координат. В декартовой системе координат:
В цилиндрической системе координат:
где При рациональном выборе начала координат и направлении координатных осей эти уравнения в рассматриваемых задачах существенно упрощаются. Например, если в цилиндрическом конденсаторе ось
Уравнение Пуассона в цилиндрических координатах принимает вид
Интегрирование такого уравнения не представляет затруднений. Постоянные интегрирования определяются из заданных граничных условий.
Пример 1. Дан плоский конденсатор с равномерно распределенным объемным зарядом Пренебрегая краевым эффектом, найти потенциал и напряженность в точках, лежащих между обкладками.
Расположим оси координат, как показано на рис. 1.2. Уравнение Пуассона в декартовой системе координат примет вид
Интегрируя это уравнение, находим
Здесь Так как конденсатор замкнут накоротко, потенциал левой и правой обкладок одинаков. Можно положить их равными нулю. При этом граничные условия формулируются в виде соотношений
Используя их, получаем
Таким образом, потенциал точки с координатой
Напряженность
Таким образом,
|
.
,
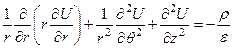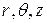- цилиндрические координаты точки.
направлена вдоль оси конденсатора, то с учетом допущения имеем:
; 
.
.
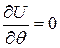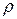между обкладками. Расстояние между обкладками равно 
(рис. 1.2). Конденсатор замкнут накоротко.
.
.
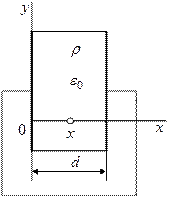
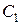и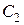 
- постоянные интегрирования, определяемые из граничных условий.
; 
.
; 
.
.
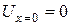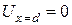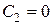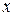
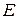находим, учитывая, что в рассматриваемой задаче при указанном расположении координатных осей
; 
.
.
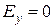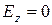