Пример. В прямоугольном пазу электрической машины находится шина высотой и ширинойВ прямоугольном пазу электрической машины находится шина высотой С учетом указанных в задании, допущений изобразим модель электромагнитной системы (рис.10.2 а).
Рис. 10.2. Модель электромагнитной системы
При бесконечной большой магнитной проницаемости ферромагнитного материала, в котором сделан паз, магнитная индукция в ферромагнитном материале будет конечная, а напряженность поля будет в нем равна нулю. Учет границ приводит к модели рис.10.2 (метод отражения). Решение приведем в декартовой системе координат. В шине напряженность магнитного поля Запишем уравнение поля для комплексов амплитуд:
Уравнения (10.1) и (10.2) для нашего случая плоской волны приводятся к уравнению
Здесь Найдем решение уравнения (10.3) Уравнение (10.3) представляет собой линейное дифференциальное уравнение второго порядка. Его решение записывают следующим образом:
где С1 и С2 – постоянные интегрирования;
Определим постоянные интегрирования. По закону полного тока при
откуда:
Тогда
Из (10.1) находим:
Подставляя числовые данные, имеем:
где
где
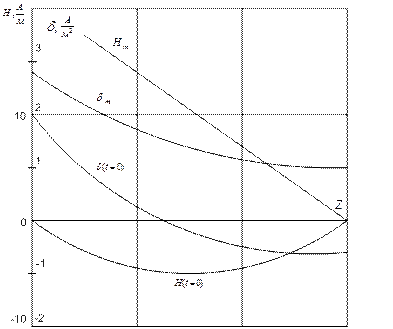
где Строим по данным расчета зависимости Определим комплексное сопротивление шины длиной Вектор Пойнтинга внешней поверхности шины:
Комплексное сопротивление:
Определяем мощность, теряемую на 1м длины шины
Рис.10.3
|
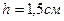и шириной 
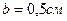. Проводимость материала шины 
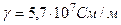, магнитная проницаемость 
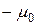частота 
, начальная фаза тока 
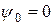, ток в шине 
.
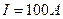направлена по оси 
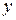, напряженность электрического поля – по оси 
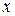. Вектор Пойнтинга направлена по оси 
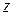. Электромагнитная волна проникает из диэлектрика в шину через наружную поверхность шины и по мере проникновения в шину затухает по амплитуде. Величины поля изменяются по гармоническому закону.
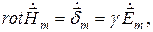(10.1)
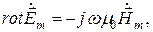(10.2)
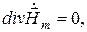(как следствие) (10.2)
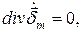(как следствие) (10.1)
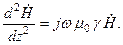(10.3)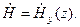
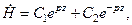(10.4)
.
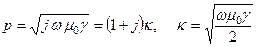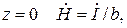при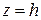 
имеем 
. Для определения постоянных интегрирования составим два уравнения:
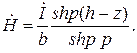(10.5)
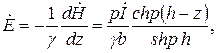(10.6)
(10.7)
,
.
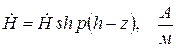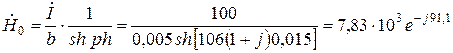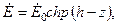
- напряженность электрического поля на нижней грани шины.
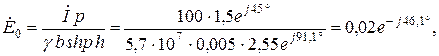
- плотность тока на нижней грани шины.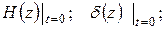
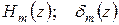(рис. 10.3).
.
.
.
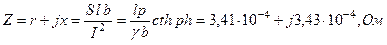