Пример. Параметры электромагнитной системы : , ; ;
Параметры электромагнитной системы: С учетом указанных в задании допущениях строится расчетная модель электромагнитной системы (рис.9.2)
Рис.9.2.
Решение приведем в цилиндрической системе координат, ось которой совпадает с осью проводника и имеет направление, совпадающее с направлением тока в рассматриваемый момент времени. В такой системе координат с учетом принятых выше допущений электромагнитное поле в проводнике имеет только осевую составляющую напряженности электрического поля, направленную вдоль линии тока и только угловую составляющую напряженности магнитного поля, поверхностное значение которой на поверхности проводника, благородя осевой симметрии системы можно рассчитать на основании закона полного тока.
Запишем уравнение Максвелла для проводящей среды в комплексной форме
совместно с остальными уравнениями электродинамики:
Будем для решения использовать понятие векторного магнитного потенциала
тогда система уравнений поля (9.2)-(9.6) сводится к уравнению для комплекса амплитуды векторного магнитного потенциала. Перепишем (9.2)и (9.3) соответственно в виде
Из (**) следует Учитывая векторное тождество
и что
где Вектор имеет только одну составляющую, т.е.
Введя параметр
Общее решение (9.9) можно записать в виде
где Так как аргумент функции Бесселя общается в нуль на оси провода и
Напряженность магнитного поля определим с учетом правила дифференцирования функций Бесселя.
Определим постоянную интегрирования. При откуда Подставляя выражение для
Напряженность электрического поля:
Комплекс амплитуды плотности тока:
Подставляя числовые данные и учитывая, что
и
получим
По получаемым выражениям (9.16) - (9.18) рассчитываются Таблица 9.2
Рис.9.3. Кривые значений Записываются выражения мгновенных величин на поверхности проводника
Строятся эти зависимости на половину периода (рис.9.4). Определяем модуль вектор Пойнтинга на поверхность провода.
Рис.9.4. Кривые изменения величин в зависимости от времени на поверхности проводника.
Используя теорему Умова-Пойнтинга, определяем: потери мощности на 1м длины проводника
величины активного сопротивления и индуктивного сопротивления, обусловленного внутренней индуктивностью проводника:
|

 ,
,  ;
;  ;
; 
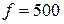 Гц;
Гц;  ;
;  .
.
 . (9.1)
. (9.1) , (9.2)
, (9.2) (9.3)
(9.3) , (9.4)
, (9.4) ; (9.5)
; (9.5) . (9.6)
. (9.6) , который вводится соотношениями
, который вводится соотношениями ,
, (*)
(*)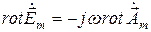 . (**)
. (**) .
.
 , из (*) получаем
, из (*) получаем (9.7)
(9.7) .
. . Поэтому (9.7) можно записать в виде
. Поэтому (9.7) можно записать в виде (9.8)
(9.8)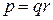 получим уравнение Бесселя с комплексным аргументом
получим уравнение Бесселя с комплексным аргументом 
 (9.9)
(9.9) , (9.10)
, (9.10) - функция Бесселя нулевого порядка соответственно первого и второго рода.
- функция Бесселя нулевого порядка соответственно первого и второго рода. =
=  , то функции Бесселя второго рода должна быть из решения исключена, т.е. постоянная
, то функции Бесселя второго рода должна быть из решения исключена, т.е. постоянная  . Тогда
. Тогда . (9.11)
. (9.11) (9.12)
(9.12) ,
, .
. в (9.12), находим
в (9.12), находим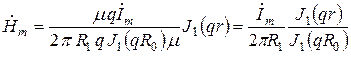 . (9.13)
. (9.13) (9.14)
(9.14)
 (9.15)
(9.15) ,
,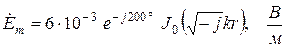 (9.16)
(9.16) (9.17)
(9.17) (9.18)
(9.18) в зависимости от значений радиуса
в зависимости от значений радиуса 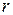 с помощью таблицы функций Бесселя (см. приложение 1). Результаты сводятся в табл.9.2. На основании полученных данных строятся кривые зависимости
с помощью таблицы функций Бесселя (см. приложение 1). Результаты сводятся в табл.9.2. На основании полученных данных строятся кривые зависимости  и
и  от
от 







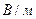



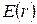 и
и  в момент времени
в момент времени 
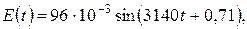



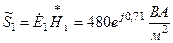



 .
.


