Указания. Для определения векторного магнитного потенциала необходимо решить уравнение Пуассона
Для определения векторного магнитного потенциала необходимо решить уравнение Пуассона
при граничных условиях на поверхности раздела сред:
Расположим оси цилиндрической системы координат так, чтобы ось Учитывая, что поле обладает круговой симметрией
где Граничные условия для данной задачи будут такими: при Решив краевую задачу (1) и (2), получается выражение для векторного потенциала (вывод студентам нужно сделать самостоятельно):
Магнитный поток через поверхность ограниченную контуром,
Построение картины поля. Число трубок индукции внутри провода рекомендуется выбрать
где Используя (3)-(5), получаем рекуррентное соотношение для радиусов линии индукции, разделяющих магнитное поле на трубки равного магнитного потока внутри провода
Радиус окружность, ограничивающей последнюю внутреннюю трубку должен получиться равному Аналогично, для радиусов огранивающих трубки внешнего магнитного потока, получаем рекуррентное соотношение где Радиус окружности
|

 ,
, и
и  .
.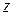 совпала с осью цилиндра. Так как вектор плотности тока имеет только одну проекцию, то и векторной потенциал будет иметь только одну проекцию на ось
совпала с осью цилиндра. Так как вектор плотности тока имеет только одну проекцию, то и векторной потенциал будет иметь только одну проекцию на ось  , для векторного потенциала имеем уравнение:
, для векторного потенциала имеем уравнение:
 (1)
(1) .
.
 ,
,  . (2)
. (2) (3)
(3) определяется
определяется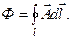 (4)
(4) Тогда поток в одной трубке равен
Тогда поток в одной трубке равен , (5)
, (5) - магнитный поток, замыкающий внутри провода (на длине
- магнитный поток, замыкающий внутри провода (на длине  ).
).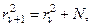 где
где 
 .
.
 - показатель геометрической прогрессии в соответствии с которой меняются радиусы;
- показатель геометрической прогрессии в соответствии с которой меняются радиусы;  - магнитный поток внешней трубки.
- магнитный поток внешней трубки. , ограничивающей первую внешнюю трубку, будет равен:
, ограничивающей первую внешнюю трубку, будет равен:  .
.


