Российской Федерации.
1.
| 2.
| 3.
| 4.
| 5.
| 6.
| 7.
| 8.
| 9.
| 10.
| 11.
| 12.
| 13.
| 14.
| 15.
| 16.
| 17.
| 18.
| 19.
| 20.
| 21.
| 22.
| 23.
| 24.
| 25.
| 26.
| 27.
| 28.
| 29.
| 30.
|
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Функциональные ряды.
Индивидуальные задания.
Волгодонск
УДК 811.111-36 (076.5)
Рецензент д.т.н., проф. Сысоев Ю.С.
Шпонарская С.Н., Кремлев А.Г. Функциональные ряды. Индивидуальные задания: учеб.-метод. пособие/ С.Н. Шпонарская, А.Г Кремлев. – Волгодонский инженерно-технический институт (ф) НИЯУ МИФИ.
Предназначено для студентов 2-го курса всех специальностей.
© ВИТИ НИЯУ МИФИ, 2012
© Коллектив авторов, 2012
Найти интервал сходимости степенного ряда и исследовать на сходимость на концах интервала.
1.  ;
| 2.  ;
| 3.  ;
| 4.  ;
| 5.  ;
| 6.  ;
| 7.  ;
| 8.  ;
| 9.  ;
| 10.  ;
| 11.  ;
| 12.  ;
| 13.  ;
| 14.  ;
| 15.  ;
| 16.  ;
| 17.  ;
| 18.  ;
| 19.  ;
| 20.  ;
| 21.  ;
| 22.  ;
| 23.  ;
| 24.  ;
| 25.  ;
| 26.  ;
| 27.  ;
| 28.  ;
| 29.  ;
| 30.  .
|
Найти интервал сходимости степенного ряда и исследовать на сходимость на концах интервала.
1.  ;
| 2.  ;
| 3.  ;
| 4.  ;
| 5.  ;
| 6.  ;
| 7.  ;
| 8.  ;
| 9.  ;
| 10.  ;
| 11.  ;
| 12.  ;
| 13.  ;
| 14.  ;
| 15.  ;
| 16.  ;
| 17.  ;
| 18.  ;
| 19.  ;
| 20.  ;
| 21.  ;
| 22.  ;
| 23.  ;
| 24.  ;
| 25.  ;
| 26.  ;
| 27.  ;
| 28.  ;
| 29.  ;
| 30.  .
|
3. Пользуясь разложением в степенной ряд, вычислить с точностью  .
1.  , =0,0001;
| 2.  , =0,001;
| 3.  , =0,0001;
| 4.  , =0,0001;
| 5.  , =0,001;
| 6.  , =0,0001;
| 7.  , =0,0001;
| 8.  , =0,001;
| 9.  , =0,0001;
| 10.  , =0,0001;
| 11.  , =0,0001;
| 12.  , =0,0001;
| 13.  , =0,000001;
| 14.  , =0,001;
| 15.  , =0,0001;
| 16.  , =0,001;
| 17.  , =0,0001;
| 18.  , =0,00001;
| 19.  , =0,0001;
| 20.  , =0,0001;
| 21.  , =0,001;
| 22.  , =0,001;
| 23.  , =0,001;
| 24.  , =0,0001;
| 25.  , =0,0001;
| 26.  , =0,0001;
| 27.  , =0,0001;
| 28.  , =0,0001;
| 29.  , =0,0001;
| 30.  , =0,00001.
|
4. Вычислить приближенно определенный интеграл с точностью , разложив подынтегральную функцию в степенной ряд.
1.  , =0,001;
| 2.  , =0,0001;
| 3.  , =0,001;
| 4.  , =0,001;
| 5.  , =0,001;
| 6.  , =0,001;
| 7.  , =0,001;
| 8.  , =0,001;
| 9.  , =0,001;
| 10.  , =0,001;
| 11.  , =0,001;
| 12.  , =0,001;
| 13.  , =0,0001;
| 14.  , =0,0001;
| 15.  , =0,001;
| 16.  , =0,001;
| 17.  , =0,001;
| 18.  , =0,0001;
| 19.  , =0,001;
| 20.  , =0,0001;
| 21.  , =0,001;
| 22.  , =0,0001;
| 23.  , =0,0001;
| 24.  , =0,001;
| 25.  , =0,0001;
| 26.  , =0,001;
| 27.  , =0,001;
| 28.  , =0,001;
| 29.  , =0,001;
| 30.  , =0,001.
|
5. Разложить в ряд Фурье на отрезке [  ;  ] периодическую функцию.
1.  ;
| 2.  ;
| 3.  ;
| 4.  ;
| 5.  ;
| 6.  ;
| 7.  ;
| 8.  ;
| 9.  ;
| 10.  ;
| 11.  ;
| 12.  ;
| 13.  ;
| 14.  ;
| 15.  ;
| 16.  ;
| 17.  ;
| 18.  ;
| 19.  ;
| 20.  ;
| 21.  ;
| 22.  ;
| 23.  ;
| 24.  ;
| 25.  ;
| 26.  ;
| 27.  ;
| 28.  ;
| 29.  ;
| 30.  .
|
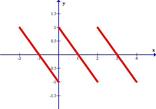
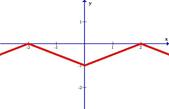
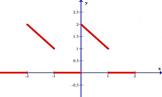
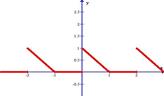
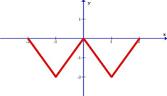
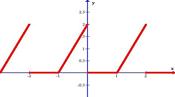
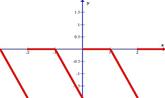
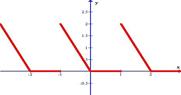
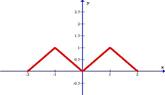
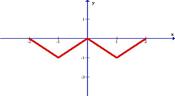
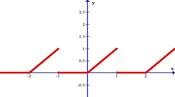
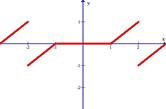
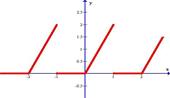
Разложить в ряд Фурье функцию, заданную графически.
1.
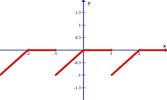
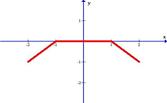
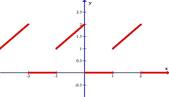
| 2.
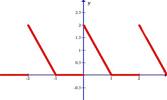
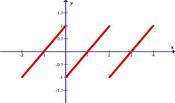
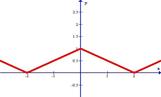
| 3.
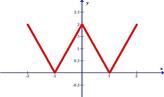
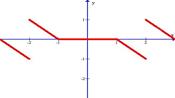
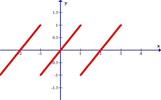
| 4.
| 5.
| 6.
| 7.
| 8.
| 9.
| 10.
| 11.
| 12.
| 13.
| 14.
| 15.
| 16.
| 17.
| 18.
| 19.
| 20.
| 21.
| 22.
| 23.
| 24.
| 25.
| 26.
| 27.
| 28.
| 29.
| 30.
|
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
|
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
|
|
Объект, субъект, предмет, цели и задачи управления персоналом Социальная система организации делится на две основные подсистемы: управляющую и управляемую...
Законы Генри, Дальтона, Сеченова. Применение этих законов при лечении кессонной болезни, лечении в барокамере и исследовании электролитного состава крови Закон Генри:
Количество газа, растворенного при данной температуре в определенном объеме жидкости, при равновесии прямо пропорциональны давлению газа...
Ганглиоблокаторы. Классификация. Механизм действия. Фармакодинамика. Применение.Побочные эфффекты Никотинчувствительные холинорецепторы (н-холинорецепторы) в основном локализованы на постсинаптических мембранах в синапсах скелетной мускулатуры...
|
|
