Функциональные ряды.
Индивидуальные задания.
Волгодонск
УДК 811.111-36 (076.5)
Рецензент д.т.н., проф. Сысоев Ю.С.
Шпонарская С.Н., Кремлев А.Г. Функциональные ряды. Индивидуальные задания: учеб.-метод. пособие/ С.Н. Шпонарская, А.Г Кремлев. – Волгодонский инженерно-технический институт (ф) НИЯУ МИФИ.
Предназначено для студентов 2-го курса всех специальностей.
© ВИТИ НИЯУ МИФИ, 2012
© Коллектив авторов, 2012
Найти интервал сходимости степенного ряда и исследовать на сходимость на концах интервала.
1.  ; ;
| 2.  ; ;
| 3.  ; ;
| 4.  ; ;
| 5. 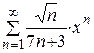 ; ;
| 6. 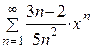 ; ;
| 7.  ; ;
| 8.  ; ;
| 9.  ; ;
| 10.  ; ;
| 11.  ; ;
| 12.  ; ;
| 13.  ; ;
| 14.  ; ;
| 15. 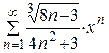 ; ;
| 16.  ; ;
| 17.  ; ;
| 18. 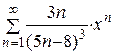 ; ;
| 19.  ; ;
| 20.  ; ;
| 21.  ; ;
| 22.  ; ;
| 23.  ; ;
| 24.  ; ;
| 25.  ; ;
| 26.  ; ;
| 27. 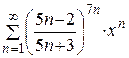 ; ;
| 28.  ; ;
| 29. 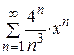 ; ;
| 30.  . .
|
Найти интервал сходимости степенного ряда и исследовать на сходимость на концах интервала.
1.  ; ;
| 2.  ; ;
| 3.  ; ;
| 4.  ; ;
| 5. 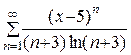 ; ;
| 6. 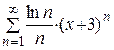 ; ;
| 7.  ; ;
| 8.  ; ;
| 9.  ; ;
| 10.  ; ;
| 11.  ; ;
| 12. 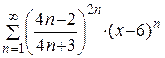 ; ;
| 13.  ; ;
| 14.  ; ;
| 15.  ; ;
| 16.  ; ;
| 17.  ; ;
| 18.  ; ;
| 19.  ; ;
| 20.  ; ;
| 21.  ; ;
| 22.  ; ;
| 23.  ; ;
| 24. 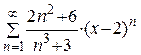 ; ;
| 25.  ; ;
| 26.  ; ;
| 27. 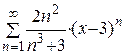 ; ;
| 28.  ; ;
| 29.  ; ;
| 30. 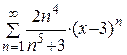 . .
|
3. Пользуясь разложением в степенной ряд, вычислить с точностью  . .
1.  , ,  =0,0001; =0,0001;
| 2.  , ,  =0,001; =0,001;
| 3.  , ,  =0,0001; =0,0001;
| 4. 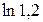 , ,  =0,0001; =0,0001;
| 5.  , ,  =0,001; =0,001;
| 6.  , ,  =0,0001; =0,0001;
| 7.  , ,  =0,0001; =0,0001;
| 8.  , ,  =0,001; =0,001;
| 9. 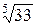 , ,  =0,0001; =0,0001;
| 10.  , ,  =0,0001; =0,0001;
| 11.  , ,  =0,0001; =0,0001;
| 12.  , ,  =0,0001; =0,0001;
| 13.  , ,  =0,000001; =0,000001;
| 14.  , ,  =0,001; =0,001;
| 15.  , ,  =0,0001; =0,0001;
| 16.  , ,  =0,001; =0,001;
| 17.  , ,  =0,0001; =0,0001;
| 18. 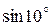 , ,  =0,00001; =0,00001;
| 19.  , ,  =0,0001; =0,0001;
| 20.  , ,  =0,0001; =0,0001;
| 21.  , ,  =0,001; =0,001;
| 22.  , ,  =0,001; =0,001;
| 23.  , ,  =0,001; =0,001;
| 24.  , ,  =0,0001; =0,0001;
| 25.  , ,  =0,0001; =0,0001;
| 26.  , ,  =0,0001; =0,0001;
| 27.  , ,  =0,0001; =0,0001;
| 28.  , ,  =0,0001; =0,0001;
| 29. 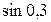 , ,  =0,0001; =0,0001;
| 30.  , ,  =0,00001. =0,00001.
|
4. Вычислить приближенно определенный интеграл с точностью  , разложив подынтегральную функцию в степенной ряд. , разложив подынтегральную функцию в степенной ряд.
1. 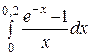 , ,  =0,001; =0,001;
| 2. 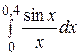 , ,  =0,0001; =0,0001;
| 3.  , ,  =0,001; =0,001;
| 4.  , ,  =0,001; =0,001;
| 5.  , ,  =0,001; =0,001;
| 6.  , ,  =0,001; =0,001;
| 7.  , ,  =0,001; =0,001;
| 8.  , ,  =0,001; =0,001;
| 9.  , ,  =0,001; =0,001;
| 10.  , ,  =0,001; =0,001;
| 11. 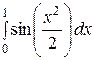 , ,  =0,001; =0,001;
| 12. 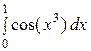 , ,  =0,001; =0,001;
| 13.  , ,  =0,0001; =0,0001;
| 14.  , ,  =0,0001; =0,0001;
| 15.  , ,  =0,001; =0,001;
| 16.  , ,  =0,001; =0,001;
| 17.  , ,  =0,001; =0,001;
| 18.  , ,  =0,0001; =0,0001;
| 19.  , ,  =0,001; =0,001;
| 20.  , ,  =0,0001; =0,0001;
| 21.  , ,  =0,001; =0,001;
| 22.  , ,  =0,0001; =0,0001;
| 23.  , ,  =0,0001; =0,0001;
| 24.  , ,  =0,001; =0,001;
| 25.  , ,  =0,0001; =0,0001;
| 26.  , ,  =0,001; =0,001;
| 27. 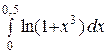 , ,  =0,001; =0,001;
| 28.  , ,  =0,001; =0,001;
| 29.  , ,  =0,001; =0,001;
| 30.  , ,  =0,001. =0,001.
|
5. Разложить в ряд Фурье на отрезке [  ; ;  ] периодическую функцию. ] периодическую функцию.
1.  ; ;
| 2.  ; ;
| 3.  ; ;
| 4.  ; ;
| 5.  ; ;
| 6.  ; ;
| 7.  ; ;
| 8.  ; ;
| 9.  ; ;
| 10.  ; ;
| 11.  ; ;
| 12.  ; ;
| 13.  ; ;
| 14.  ; ;
| 15.  ; ;
| 16.  ; ;
| 17.  ; ;
| 18.  ; ;
| 19.  ; ;
| 20.  ; ;
| 21. 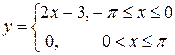 ; ;
| 22.  ; ;
| 23.  ; ;
| 24.  ; ;
| 25.  ; ;
| 26.  ; ;
| 27.  ; ;
| 28.  ; ;
| 29.  ; ;
| 30.  . .
|
Разложить в ряд Фурье функцию, заданную графически.
1.

| 2.

| 3.

| 4.

| 5.
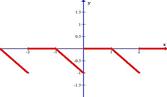
| 6.
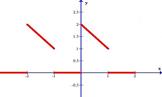
| 7.

| 8.

| 9.
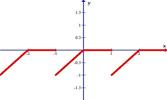
| 10.

| 11.

| 12.

| 13.

| 14.

| 15.

| 16.

| 17.

| 18.
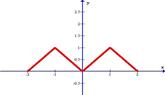
| 19.

| 20.

| 21.

| 22.

| 23.
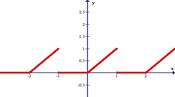
| 24.

| 25.

| 26.

| 27.

| 28.

| 29.

| 30.

|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Принципы и методы управления в таможенных органах Под принципами управления понимаются идеи, правила, основные положения и нормы поведения, которыми руководствуются общие, частные и организационно-технологические принципы...
ПРОФЕССИОНАЛЬНОЕ САМОВОСПИТАНИЕ И САМООБРАЗОВАНИЕ ПЕДАГОГА Воспитывать сегодня подрастающее поколение на современном уровне требований общества нельзя без постоянного обновления и обогащения своего профессионального педагогического потенциала...
Эффективность управления. Общие понятия о сущности и критериях эффективности. Эффективность управления – это экономическая категория, отражающая вклад управленческой деятельности в конечный результат работы организации...
|
Потенциометрия. Потенциометрическое определение рН растворов Потенциометрия - это электрохимический метод исследования и анализа веществ, основанный на зависимости равновесного электродного потенциала Е от активности (концентрации) определяемого вещества в исследуемом растворе...
Гальванического элемента При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов...
Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века...
|
|

 ;
;
 ;
;
 ;
;
 ;
;
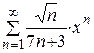 ;
;
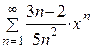 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
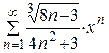 ;
;
 ;
;
 ;
;
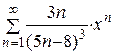 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
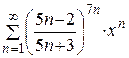 ;
;
 ;
;
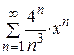 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
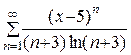 ;
;
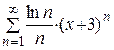 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
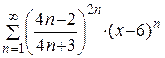 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
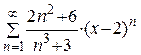 ;
;
 ;
;
 ;
;
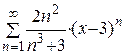 ;
;
 ;
;
 ;
;
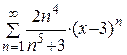 .
.
 .
. ,
,  ,
,  ,
, 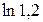 ,
,  ,
,  ,
,  ,
,  ,
, 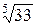 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 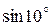 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 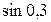 ,
,  ,
, 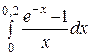 ,
, 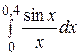 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 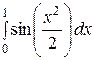 ,
, 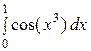 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 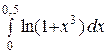 ,
,  ,
,  ,
,  ,
,  ;
;  ] периодическую функцию.
] периодическую функцию. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
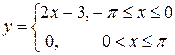 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

































