Уравнение состояния идеальных газов
http//:mivmeste.org.ua Математическая запись универсального газового закона проста: pV = nRT * Она содержит основные характеристики поведения газов: p, V и T — соответственно давление, объем и абсолютная температура газа (в градусах Кельвина), R — универсальная газовая постоянная, общая для всех газов, а n — число, пропорциональное числу молекул или атомов газа (так называемое число молей газа — см. Закон Авогадро). Чтобы понять, как работает этот закон, давайте представим, что температура газа постоянна. В этом случае в правой части уравнения получается константа. Значит, произведение давления и объема при неизменной температуре оказывается неизменным. Повышение давления сопровождается уменьшением объема, и наоборот. Это не что иное, как закон Бойля—Мариотта — одна из первых экспериментально полученных формул, описывающих поведение газов. С другой стороны, при постоянном давлении (например, внутри воздушного шарика, где давление газа равно атмосферному) повышение температуры сопровождается увеличением объема. А это — закон Шарля, другая экспериментальная формула поведения газов. Закон Авогадро и закон Дальтонатакже являются следствиями универсального газового закона. Этот закон представляет собой то, что в физике принято называть уравнением состояния вещества, поскольку он описывает характер изменения свойств вещества при изменении внешних условий. Строго говоря, этот закон в точности выполняется только для идеального газа. Идеальный газ представляет собой упрощенную математическую модель реального газа: молекулы считаются движущимися хаотически, а соударения между молекулами и удары молекул о стенки сосуда — упругими, то есть не приводящими к потерям энергии в системе. Такая упрощенная модель очень удобна, поскольку позволяет обойти очень неприятную трудность — необходимость учитывать силы взаимодействия между молекулами газа. И это себя оправдывает, поскольку в природных условиях поведение большинства реальных газов практически не отличается от поведения идеального газа — отклонения в поведении практически всех природных газов, например атмосферного азота и кислорода, от поведения идеального газа не превышают 1%. Это позволяет ученым спокойно включать уравнение состояния идеального газа даже в весьма сложные теоретические расчеты. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. (Заметьте, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. А дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия — то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов.) В будущем, по мере совершенствования теоретических методов, возможно, будут выведены более точные уравнения для описания состояния реальных газов с учетом их характеристик на молекулярном уровне. * Эта формула была получена в 1874 годуД. И. Менделеевым путем объединения закона Авогадро и общего газового закона (pV / T = const), сформулированного в 1834 году Б. П. Э. Клапейроном. Поэтому этот закон (в Европе, по крайней мере) принято называть законом Менделеева—Клапейрона. По существу, этот закон позволил ввести все ранее сделанные эмпирические заключения о характере поведения газов в рамки новой молекулярно-кинетической теории. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеМенделеева — Клапейрона) — формула, устанавливающая зависимость междудавлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
где · · · · Так как
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. Уравнение, выведенное Клапейроном содержало некую неуниверсальную газовую постоянную
Менделеев же обнаружил, что Связь с другими законами состояния идеального газа [править] В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
А в форме пропорции Уравнение состояния идеального газа и универсальная газовая постоянная Уравнение состояния газа устанавливает зависимость между основными параметрами состояния газов р, v и Т. Зависимость между этими параметрами, характеризующими состояние газов, устанавливается из закона Бойля - Мариотта и Гей-Люссака. Предположим, что идеальный газ массой 1 кг с. начальными параметрами р1, v1 и Т1 переходит в новое состояние, характеризуемое параметрами р1, v1 и Т1. Этот переход происходит сначала при постоянном давлении p1 до некоторого промежуточного объема v’ а затем при постоянной температуре Т2 до конечного объема v2. Изменение состояния газа при постоянном давлении, согласно закону Гей-Люссака, v1/v' = T1/T2, откуда v' = v1T2/T1. Изменение состояния газа при постоянной температуре, согласно закону Бойля - Мариотта v'/v2 = p2/p1, откуда v' = p2v2/p1. Приравнивая уравнения, получим v1T2/T1 = p2v2/p1. Умножив обе части уравнения на р1/Т2, получим p1 v1 T2/(T1 T2) = p1 p2 v2/(p1 T2), или p1 v1/ T1 = p2 v2/ T2 = pv / T = const. Постоянную величину const называют удельной газовой постоянной и обозначают буквой R, тогда уравнение примет вид pv /T = Rилиpv = RT. Это уравнение называют уравнением состояния идеального газа или уравнением Клапейрона. Его называют также характеристическим уравнением для 1 кг массы газа. [ R ] = [ pv/T ] = Па * м3/(кг*К) = Дж/ (кг*К). Уравнение состояния для произвольного количества идеального газа получается умножением обеих частей его на массу газа М с учетом, что V = vМ, где V - объем газа, м3, т. е. pV = MRT. Уравнение состояния для 1 кмоля газа получается умножением обеих частей его на молекулярную массу, т. е. npv = nRT.ПолучаемnR = npv/T.Величина nR для всех идеальных газов одинакова и ее называют универсальной газовой постоянной. Значение универсальной газовой постоянной при нормальных R0 = nR = 22,4*101325/273 = 8314,3 Дж/ (кмоль*К) Определим удельную газовую постоянную R = 8314,3p,Дж/ (кг*К).
|

 ,
, — давление,
— давление, — молярный объём,
— молярный объём, — универсальная газовая постоянная
— универсальная газовая постоянная — абсолютная температура,К.
— абсолютная температура,К. , где
, где 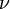 — количество вещества, а
— количество вещества, а  , где
, где  — масса,
— масса,  —молярная масса, уравнение состояния можно записать:
—молярная масса, уравнение состояния можно записать: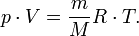
 , значение которой необходимо было измерять для каждого газа:
, значение которой необходимо было измерять для каждого газа:


 — закон Бойля — Мариотта.
— закон Бойля — Мариотта. — Закон Гей-Люссака.
— Закон Гей-Люссака. — закон Шарля (второй закон Гей-Люссака, 1808 г.)
— закон Шарля (второй закон Гей-Люссака, 1808 г.) этот закон удобен для расчёта перевода газа из одного состояния в другое.
этот закон удобен для расчёта перевода газа из одного состояния в другое.


