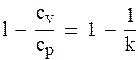Изобарический процесс

Изобарным процессом называют процесс, проходящий при постоянном давлении (р = const). Следовательно, в этом процессе происходит внешняя работа расширения газа.

В соответствии с первым законом термодинамики будем иметь

 

 

Работа расширения определится из выражения d l = pdv следующим образом:

 

 

Следовательно, в pv-координатах изобарный процесс изобразится прямой линией, параллельной оси абсцисс (рисунок 1.10).

Из уравнения состояния pv = RT можно найти соотношение между параметрами v и T

 

Откуда по закону Гей-Люссака

 

 

Значит, изменение удельного объема прямо пропорционально изменению температуры.

Работа в изобарном процессе для идеального газа, учитывая характеристическое уравнение pV = MRT, будет равна

Или

 

Тогда

 

Или

 

 

 

где разности температур относятся к одним и тем же состояниям газа и поэтому равны между собой, а сокращение дает

ср – сv = R. (1.67)

Уравнение (1.67) часто называют уравнением Майера.

Из уравнений dq = cvdT + pdv и dq = du + d l следует, что, например, в процессе изобарного расширения часть теплоты идет на увеличение внутренней энергии, так как в этом процессе температура повышается, а часть теплоты идет на работу расширения, так как удельный объем увеличивается. Для определения доли теплоты, расходуемой на внешнюю работу, разделим все члены последнего уравнения на dq, в результате получим

 

откуда с учетом du = cvdT, dq = cpdT и cp/cv = k, получим

 

 

Уравнение изобары в Ts-координатах

1.69

 

 

Формула (1.69) представляет собой уравнение логарифмической кривой (рисунок 1.11). По структуре уравнение изобары подобно уравнению изохоры.

Для случая подвода тепла к газу в изобарном процессе (1-2') в Ts-координатах изобара располагается ниже изохоры (1-2), для случая отвода тепла – выше ее. В обоих случаях линия изохоры идет круче линии изобары. Отличие заключается в коэффициентах перед логарифмами, равных теплоемкостям сp и сv. Так как сp > сv, то при одних и тех же температурах T1 и T2 изменение энтропии в изобарном процессе больше (s2 – s1)р > (s2 – s1)v, чем в изохорном процессе.