Истинная и средняя теплоемкости
Теплоемкость является функцией параметров состояния – давления и температуры, поэтому в технической термодинамике различают истинную и среднюю теплоемкости. Теплоемкость идеального газа зависит только от температуры и по определению может быть найдена лишь в интервале температур В справочной литературе зависимость истинных теплоемкостей ср и сv от температуры задают в виде таблиц и аналитических зависимостей. Аналитическую зависимость (например, для массовой теплоемкости) обычно представляют в виде полинома:
Тогда количество подведенной в процессе теплоты в интервале температур [ t1,t2 ] определяется интегралом: При исследовании термодинамических процессов часто определяют среднее в интервале температур значение теплоемкости. Она представляет собой отношение количества подведенной в процессе теплоты Q12 к конечной разности температур:
Тогда, если задана зависимость истинной теплоемкости от температуры, в соответствии с (2):
Часто в справочной литературе приводят значения средних теплоемкостей ср и сv для интервала температур от 0 до tоС. Как и истинные, их представляют в виде таблиц и функций:
При подстановке значения температуры t в эту формулу будет найдена средняя теплоемкость в интервале температур [ 0,t ]. Чтобы найти среднее значение теплоемкости в произвольном интервале [ t1,t2 ], пользуясь зависимостью (4), нужно найти количество теплоты Q12, подведенной к системе в этом интервале температур. На основании известного из математики правила интеграл в уравнении (2) может быть разбит на следующие интегралы:
Но Тогда
|

 . Однако всегда можно предположить, что этот интервал очень мал вблизи какого-либо значения температуры. Тогда можно сказать, что теплоемкость определена при данной температуре. Такая теплоемкость называется истинной.
. Однако всегда можно предположить, что этот интервал очень мал вблизи какого-либо значения температуры. Тогда можно сказать, что теплоемкость определена при данной температуре. Такая теплоемкость называется истинной.
 . (2)
. (2) . (3)
. (3)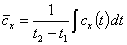 .
. (4)
(4) .
. , а
, а 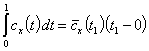 .
.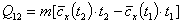 .
.


