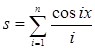Пример выполнения лабораторной работы. Для примера рассмотрим функцию у= , разложенную в сумме ряда (количество слагаемых n=40)Для примера рассмотрим функцию у= В подсчете суммы s можно увидеть закономерность. Например, следующее слагаемое суммы будет выглядеть: Подобную сумму легко посчитать, используя цикл. На каждом шаге цикла к s будет прибавляться новое слагаемое и по окончанию цикла в s будет храниться итоговая сумма всех n слагаемых Блок-схема решения:
Код программы будет следующим: setlocale(LC_ALL, "Russian"); double x = 0; // объявляем переменную x для получения от пользователя числа printf(“Введите x:”) scanf(“%lf”, x); // запрашиваем у пользователя значение double y = log(abs(2.0 * sin(x / 2))) * (-1); // высчитываем значение y по полученному значению x double s = 0; int i = 1; int n = 40; // задаем начальные значения для цикла while (i <= n) { s += cos(i * x) / i;// к s прибавляем слагаемое на i-м шаге i++; // увеличиваем счетчик i на единицу } printf(“y = %lf s = %lf”, y, s); // выводим что получилось на экран
Разбиение задач по вариантам
|
, разложенную в сумме ряда 
(количество слагаемых n=40). Заметим, что значения s и y при одинаковых значениях x будут приблизительно равными.
. А сумма для n слагаемых можно записать в виде: 
