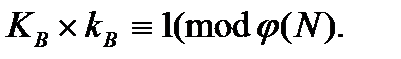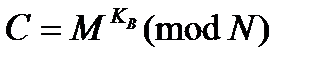Теоретическое введение. Алгоритм RSA предложен в 1978 г
Алгоритм RSA предложен в 1978 г. тремя авторами: Р. Райвестом, А. Шамиром и А. Адлеманом. Это первый полноценный алгоритм работы с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме цифровой подписи. Надежность алгоритма RSA основана на трудности факторизации больших чисел и вычисления дискретных логарифмов в конечных полях. В криптосистеме RSA открытый ключ КВ, секретный ключ kB, сообщение М и криптограмма С принадлежат множеству целых чисел ZN={0,1,2,…,N-1} где N – модуль: N=P´Q В данном случае P и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают P и Q равной длины и хранят в секрете. Множество ZN с операциями сложения и умножения по модулю N образует арифметику по модулю N. Открытый ключ КВ выбирают случайным образом так, чтобы выполнялись следующие условия:
где Функция Эйлера Второе из указанных условий означает, что открытый ключ КВ и функция Эйлера Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ kB такой, что
или
Это можно осуществить, так как получатель сообщения В знает пару простых чисел P и Q и может легко найти Открытый ключ KB используется для шифрования сообщения, а секретный ключ kB – для расшифрования. Шифрование определяет криптограмму С через пару (открытый ключ КВ, сообщение М) в соответствии со следующей формулой:
В качестве алгоритма быстрого вычисления значения С используется ряд последовательных возведений в квадрат целого М и умножений на М с приведением по модулю N. Определение значения М по известным С, КВ и N практически не осуществимо при Однако обратную задачу, т.е. задачу расшифрования криптограммы С можно решить, используя пару (секретный ключ kB, криптограмма С) по формуле:
Подставляя в данную формулу значение для С, получаем:
Величина
или в несколько более общей форме
Учитывая вышесказанное, получаем:
Таким образом, если криптограмму
возвести в степень kB, то в результате получим исходное открытое сообщение М, так как
Таким образом, получатель В, создавая криптограмму С, защищает два параметра: секретный ключ kB, пару чисел (P, Q), произведение которых дает значение модуля N. Противнику известны лишь значения КВ и N. Если бы он смог разложить число N на множители, то, узнав тройку чисел (P, Q, KB), вычислил значение Для алгоритма RSA этап создания ключей состоит из следующих операций: 1. Выбираются два простых числа p и q 2. Вычисляется их произведение n=(p´q) 3. Выбирается произвольное число e (e<n), такое, что НОД (e,(p-1)(q-1))=1, то есть e должно быть взаимно простым с числом (p-1)(q-1). 4. Методом Евклида решается в целых числах уравнение e ´d+(p-1)(q-1) ´y=1. Здесь неизвестными являются переменные d и y – метод Евклида как раз и находит множество пар (d,y), каждая из которых является решением уравнения в целых числах. 5. Два числа (e,n) – публикуются как открытый ключ. 6. Число d хранится в строжайшем секрете – это и есть закрытый ключ, который позволит читать все послания, зашифрованные с помощью пары чисел (e,n).
|

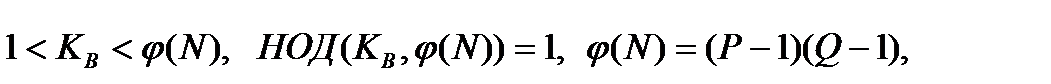
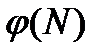 – функция Эйлера.
– функция Эйлера.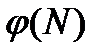 указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N.
указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N.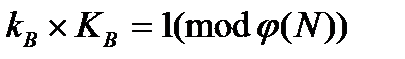
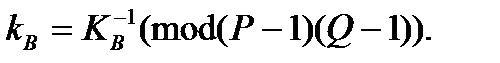

 .
.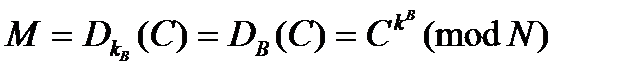 .
.

 .
.