Метод падающего груза
Применение этого метода наиболее целесообразно для двигателей с небольшими потерями вращения, что имеет место в асинхронных машинах с подшипниками качения. Экспериментальное определение момента инерции методом падающего груза проводят следующим образом: На шкив с радиусом R наматывается несколько витков шнура, на конце которого подвешивается груз G. Падая с заранее известной высоты h, он сообщает вращающимся частям угловое ускорение. Зная вес груза G, высоту падения h и время падения t, нетрудно определить момент инерции J или маховый момент GD2 исследуемого двигателя. При определении J или GD2 исходят из следующих соображений: при неподвижном роторе или при движении ротора с установившейся скоростью под действием груза момент на валу электродвигателя равен:
где R – радиус шкива, м.
Если же движение под действием груза происходит с ускорением, то часть силы тяжести груза идет на сообщение ускорения самому грузу:
а часть – на угловое ускорение (dw/dt) ротора с маховыми массами
при этом потерями вращения пренебрегаем. В свою очередь динамический момент сопротивления привода равен:
Теперь, исходя из того, что крутящий момент и момент сопротивления на валу электродвигателя равны, запишем:
а так как
то
Откуда получаем:
Так как движение происходит под действием постоянной силы, создаваемой грузом, то имеет место равномерно-ускоренное движение, величина ускорения которого равна:
откуда
А так как
то
Откуда:
где С1 и С2 определяются из начальных условий.
При t = 0 скорость V = 0 и расстояние h = 0, тогда C1 = 0 и С2 = 0. Подставив С1 и С2 в выражение (26), получим:
Откуда:
Выражение (28) подставим в (21):
Так как маховый момент
а
то
Таким образом, выражения (29) и (30) позволяют, выполнив необходимые измерения экспериментально определить момент инерции привода и маховый момент соответственно.
Если же потери вращения достаточно велики, и ими пренебречь нельзя, то поступают следующим образом: определяют величину момента трения путем постепенного увеличения веса груза на шнуре до G0, т.е. до величины, когда двигатель будет находиться на грани трогания, а вес G0 будет уравновешивать силы трения (здесь сила трения принимается независимой от скорости вращения, что справедливо при малых скоростях). Зная величину силы трения можно теперь определить величину момента инерции, учтя, что момент, создаваемый подвешенным грузом, расходуется не только на преодоление динамического момента сопротивления, но и на преодоление момента трения, равного:
откуда
|

 , Н×м, (14)
, Н×м, (14)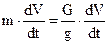 , (15)
, (15)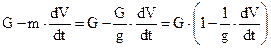 , (16)
, (16) . (17)
. (17) , (18)
, (18)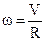 , (19)
, (19) . (20)
. (20) . (21)
. (21)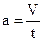 , (22)
, (22) . (23)
. (23)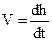 , (24)
, (24)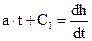 . (25)
. (25)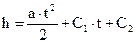 , (26)
, (26) . (27)
. (27)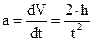 . (28)
. (28) , кг×м2. (29)
, кг×м2. (29)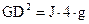 ,
,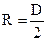 ,
,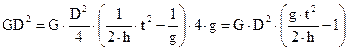 , Н×м2. (30)
, Н×м2. (30) , (31)
, (31)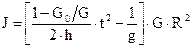 . (32)
. (32)


