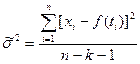Задание по УИРС
а) Получить функцию б) При анализе стабильности по одной реализации проанализировать точность прогнозирования в) Провести аналогичный сравнительный анализ при числе наблюдений
Требования к отчету Отчет должен содержать: формулировку цели работы, расчетные формулы, таблицы измерений и расчетных характеристик, зависимости
Литература 1. ГОСТ 15895-77. Статистические методы управления качеством продукции. Термины и определения. M.: Издательство стандартов, 1977. 2. ГОСТ 16304-74. Управление технологическими процессами. Контроль точности технологических процессов. М.: Издательство стандартов, 1974. 3. Глудкин О.П., Черняев В.Н.. Анализ и контроль технологических процессов производства РЭА. М.: Радио и связь, 1983. 4. ГОСТ 16467-70. Статистические показатели точности и стабильности технологических операций. Методы расчета. М.: Издательство стандартов, 1970. 5. ГОСТ 11006-74. Правила проверки согласия опытного распределения с теоретическим. М.: Издательство стандартов, 1974. 6. ГОСТ 16305-74. Контроль точности технологических процессов. Методы оценки точности в условиях серийного и массового производства. М.: Издательство стандартов, 1974. 7. Контроль и регулировка РЭА. Лабораторные работы /Дмитриевский Е.С., Илларионов О.И., Лебедев K.М. /ЛИАП.Л., I980.
Приложение I
I. Вычисление среднего значения и среднеквадратического отклонения. Расчеты производятся по формулам: - среднее - среднеквадратическое отклонение
Приложение 2
ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ(МНК)
Если имеется последовательность значений исследуемой величины При использовании сглаживающего полинома первой степени
В лабораторной работе сглаженные кривые используются для иллюстрации относительных изменений во времени среднего и среднеквадратического отклонений в ходе наблюдений, поэтому начало отсчета времени можно выбрать произвольно, в частности, так, чтобы
Указанный подход справедлив при нечетных n.
Формулы для a и b упрощаются:
При использовании сглаживающего полинома 2-й степени
Выбор вида сглаживающей функции необходимо производить, исходя из величины дисперсии
|

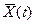 получить по МНК для сглаживающего полинома 2-й степени, определить коэффициент достоверности аппроксимации сглаживания полиномами первой и второй степени
получить по МНК для сглаживающего полинома 2-й степени, определить коэффициент достоверности аппроксимации сглаживания полиномами первой и второй степени  , сравнивая их сделать вывод о наилучшем полиноме сглаживания.
, сравнивая их сделать вывод о наилучшем полиноме сглаживания. по МНК при изменении числа обрабатываемых наблюдений с 5 по 7.
по МНК при изменении числа обрабатываемых наблюдений с 5 по 7.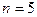 для сглаживающего полинома первой и второй степени.
для сглаживающего полинома первой и второй степени.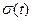 для случаев одной реализации и нескольких реализаций, значения оценок прогноза, выводы по работе, содержащие числовые характеристики стабильности
для случаев одной реализации и нескольких реализаций, значения оценок прогноза, выводы по работе, содержащие числовые характеристики стабильности 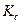 и
и  .
.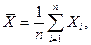
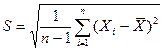 .
.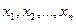 , полученных в моменты временя
, полученных в моменты временя  , то сглаживающие полиномы необходимо получать по методу наименьших квадратов (МНК),.
, то сглаживающие полиномы необходимо получать по методу наименьших квадратов (МНК),.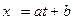 , коэффициенты определяются по формулам [6]:
, коэффициенты определяются по формулам [6]: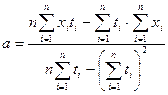 ;
;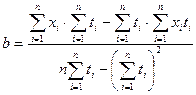 .
. . При одинаковых интервалах времени между наблюдениями моменты измерений (для n = 5) будут расположены в соответствии о таблицей:
. При одинаковых интервалах времени между наблюдениями моменты измерений (для n = 5) будут расположены в соответствии о таблицей: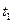
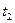

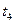

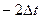
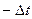
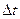
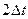
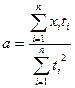 ;
; 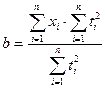 .
.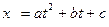 и условия
и условия 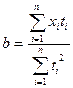 ;
; 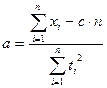 ;
; 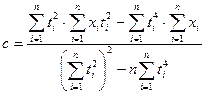 .
.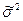 разброса наблюдений относительно сглаживающей функции
разброса наблюдений относительно сглаживающей функции 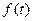 . Для сглаживающих полиномов k-й степени:
. Для сглаживающих полиномов k-й степени: