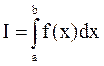Решение систем уравнений
Рассмотрим решение системы линейных уравнений с N неизвестными (
методом Гаусса. Сущность метода заключается в преобразовании исходной системы в треугольную путем последовательного исключения неизвестных x при помощи дополнительных множителей к коэффициентам a и вычитания нижестоящих строк системы из вышестоящих.
Из треугольной системы, начиная с последнего уравнения, последовательно находятся Алгоритм метода представлен в блок-схеме:
В первой половине алгоритма происходит построение треугольной матрицы (m – дополнительные множители), а во второй – расчет корней системы x1…xN. Расчет определенных интегралов Задача расчета определенного интеграла вида
сводится к определению площади фигуры, ограниченной графиком функции f(x), осью x и вертикалями, опущенными на ось x в границах интервала интегрирования:
Для определения площади фигура разбивается на элементарные фрагменты с определенным шагом h по оси x. Общая площадь определяется суммой площадей элементарных фрагментов. Площадь каждого фрагмента легко определить, если задать упрощенный вид его "верхней" границы. В зависимости от способа задания этой границы существует несколько методик расчета определенных интегралов.
|

 )
)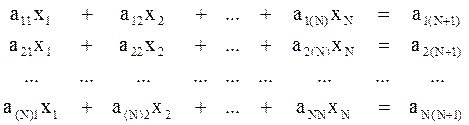

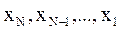 .
.