Лабораторные работы. № 1.11. Исследование законов колебательного движения физического маятника и определение ускорения свободного падения
№ 1.11. Исследование законов колебательного движения физического маятника и определение ускорения свободного падения № 1.12. Определение ускорения свободного падения с помощью математического и оборотного маятников № 1.13. Определение приведенной длины физического маятника и ускорения свободного падения № 1.14. Изучение резонансных явлений при колебаниях плоской пружины Теоретический минимум
Контрольные задания Вариант 1 1. Уравнение гармонических колебаний точки
Каков период этих колебаний? 2. Уравнение колебаний материальной точки массой
Найти максимальную силу, действующую на точку. 3. Однородный диск радиусом R совершает колебания около горизонтальной оси, проходящей на расстоянии R/2 от центра диска. Чему равна циклическая частота колебаний диска? 4. Материальная точка участвует в двух взаимно перпендикулярных колебаниях согласно уравнениям
Какова траектория результирующего движения точки? 5. Амплитуда затухающих колебаний уменьшилась в е раз за 50 колебаний. Каков логарифмический декремент затухания? 6. Период Т0 собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период Т того же маятника стал равным 0,56 с. Какова резонансная частота колебаний?
Вариант 2 1. Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимального значения? 2. Найти отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для момента, когда смещение точки от положения равновесия 3. Обруч радиуса R совершает малые колебания относительно оси, проходящей через его край. Каков период этих колебаний? 4. Складываются два взаимно перпендикулярных колебания с одинаковыми частотами. При какой разности фаз результирующее колебание будет линейным? 5. Затухающие колебания описываются уравнением
График колебания представлен на рисунке. Определите время релаксации.
6. Уравнение движения системы имеет вид
Чему равен период установившихся вынужденных колебаний системы? Вариант 3 1. Скорость материальной точки, совершающей гармонические колебания, задается уравнением
Записать зависимость смещения этой точки от времени. 2. За какое время тело, совершающее колебание с периодом Т, проходит первую половину пути от среднего значения до крайнего? 3. Однородный стержень длиной 4. Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Чему равна разность фаз складываемых колебаний? 5. Начальная амплитуда колебания маятника А0=3см. Через t1=10c она равна А1=1см. Через какой промежуток времени она станет равной А2=0,3см? 6. Изобразить резонансные кривые А(
Вариант 4 1. Уравнение движения точки
Найти период колебаний, максимальную скорость и максимальное ускорение точки. 2. Найти отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для момента времени t=T/6. 3. Однородный диск радиусом R подвешен за край. Чему равна частота его малых колебаний? 4. Точка участвует в двух одинаково направленных колебаниях, данных уравнениями
Начертить векторную диаграмму сложения амплитуд. Найти амплитуду и начальную фазу результирующего колебания. 5. Логарифмический декремент затухания математического маятника 6. Чему равна резонансная амплитуда Арез = А(ωрез) у системы без трения? Вариант 5 1. Колебания материальной точки совершаются по закону
Определить наибольшие значения скорости и ускорения. 2. Груз массой m осторожно прикрепляют к концу свободно висящей пружины. Когда груз освобождают, он опускается на 30см, а затем начинает колебаться. Чему равна частота колебаний? 3. Физический маятник представляет собой тонкий однородный стержень длиной 4. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями
Найти уравнение траектории точки. 5. Амплитуда затухающих колебаний маятника за 5 минут уменьшилась в два раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь раз? 6. Найти приближенное значение Арез при
|

 .
.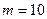 г имеет вид
г имеет вид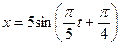 см.
см. и
и  .
.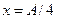 .
. .
.
 .
. .
. совершает малые колебания относительно оси, проходящей через его край. Какова частота этих колебаний?
совершает малые колебания относительно оси, проходящей через его край. Какова частота этих колебаний? ) для трех коэффициентов затухания
) для трех коэффициентов затухания  .
. см.
см. см и
см и  см.
см. . Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника? см.
см. и массой m с укрепленным на его конце маленьким шариком массой m. Маятник совершает колебания относительно горизонтальной оси, проходящей через центр стержня. Каков период гармонических колебаний маятника?
и массой m с укрепленным на его конце маленьким шариком массой m. Маятник совершает колебания относительно горизонтальной оси, проходящей через центр стержня. Каков период гармонических колебаний маятника?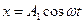 и
и  , где А1=2см, А2=1см.
, где А1=2см, А2=1см. .
.


