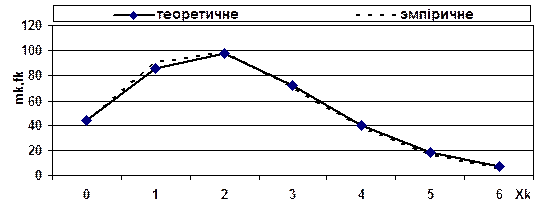
Значення показників динамічного ряду для збільшених інтервалів часу
Аналіз значень абсолютних приростів показує, що вони відносно стабільні. Тому динамічний ряд приблизно можна вирівняти за прямою. Для підрахунку необхідних сум
Таблиця №4.6. Розрахунок показників вирівняного ряду динаміки
Підставляючи у формули (4.18-4.19) суми з таблиці №4.6., одержимо:
Звідси рівняння початкової прямої буде:
Шляхом підстановки в це рівняння відповідних значень (див. графу 3 таблиці №4.6.) знайдемо вирівняні рівні Yi. Так для і = 3 одержимо:
Як бачимо з порівняння результатів сум граф 2 і 6 таблиці №10, значення сум
Таким чином, в наступному році очікується біля 886 викликів. Одержані вирівняні рівні ряду та його прогнозне значення наносимо на графік (рис.4.2). Середня кількість викликів пожежних підрозділів у добу
де xk – кількість викликів у добу; mk –кількість діб із зазначеною кількістю викликів, або
-де Nв – загальна кількість викликів за аналізований період часу; Nс –кількість діб в даному періоді. Застосування величини для розрахунку необхідної кількості пожежних автомобілів за допомогою методів теорії масового обслуговування можливо лише тоді, коли реальні потоки викликів пожежних підрозділів у місті досить добре описується законом Пуассона. Для перевірки гіпотези про пуассонівський характер потоків викликів пожежно-рятувальних підрозділів у місті необхідно за допомогою відповідних критеріїв згоди, шляхом складання графіків розподілу оцінити ступінь близькості отриманих емпіричних розподілів до передбачуваного теоретичного (до розподілу Пуассона). Теоретичний розподіл кількості діб з тією або іншою кількістю викликів пожежно-рятувальних підрозділів за аналізований період часу можна знайти за формулою:
де
Співставлення емпіричного розподілу кількості діб mk і теоретичного розподілу здійснюється за допомогою критерію Романовського, що дозволяє визначити, чи є наявними або випадковими розбіжності між розподіленнями або вони закономірні:
де k =n-2 – число ступенів свободи;
Якщо величина критерію Романовського менше 3, то розбіжність між емпіричними і теоретичними розподілами несуттєва, і прийнятий закон розподілу може служити моделлю емпіричних даних. Приклад. Надано (таблиця 4.7) розподіл викликів пожежно-рятувальних підрозділів за добами року. Потрібно графічно зобразити даний розподіл, визначити середню кількість викликів за добу, побудувати математичну модель потоку викликів і перевірити її відповідність емпіричним даним. Таблиця 4.7
Примітка. Значення fk проставляється в таблицю 4.7 після відповідних розрахунків. Будуємо полігон емпіричного розподілу кількості викликів (рисунок 4.3).
Рисунок 4.3 Розподіл кількості викликів на інтервалі
|

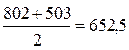
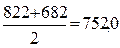
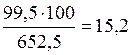

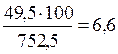
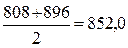
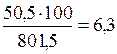
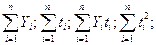 складемо розрахункову таблицю №4.6.
складемо розрахункову таблицю №4.6.


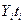
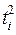
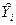
 Сума
Сума

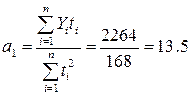
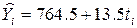
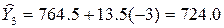
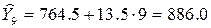
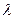 розраховується на підставі дискретного варіаційного ряду табл. 3.2 гр.4 за формулами:
розраховується на підставі дискретного варіаційного ряду табл. 3.2 гр.4 за формулами: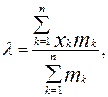 (4.20)
(4.20)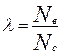 , (4.21)
, (4.21)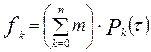 , (4.22)
, (4.22)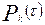 - теоретична імовірність тієї або іншої кількості викликів к=0,1,2,3…n, на інтервалі часу
- теоретична імовірність тієї або іншої кількості викликів к=0,1,2,3…n, на інтервалі часу 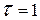 доба;
доба;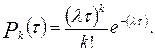 (4.23)
(4.23)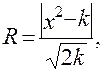 (4.24)
(4.24)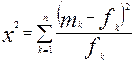 - критерій Пірсона. (4.25)
- критерій Пірсона. (4.25)