Числовые характеристики случайных величин.
Случайные величины помимо законов распределения, могут также описываться числовыми характеристиками, среди которых различают характеристики положения (математическое ожидание, мода, медиана и др.) и характеристики рассеяния (дисперсия, среднеквадратичное отклонение, различные моменты распределения порядка выше первого и др.) Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа случайной величины X формулой
Вероятностный смысл математического ожидания таков: математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Если производятся независимые испытания, в каждом из которых вероятность появления события Задача 1. Бросаются две симметричные игральные кости. Х - сумма очков на двух костях. Найти математическое ожидание Решение: Обозначим Вероятность каждого события равна
Отклонением называют разность между случайной величиной и её математическим ожиданием:
Определение. Дисперсией  случайной величины случайной величины  называется неотрицательное число называется неотрицательное число  , определяемое формулой , определяемое формулой
Определение. Средним квадратическим отклонением называют Вероятностный смысл дисперсии. Дисперсия характеризует разброс (рассеяние) значений случайной величины. Если производятся независимые испытания, в каждом из которых вероятность появления события
Для распределения Пуассона характерной особенностью является совпадение математического ожидания и дисперсии, причем
Задача 2. Дана плотность распределения Решение:
Функция плотности
При начальных условиях и
Зная
По формуле
Ответ:
|


 постоянна и равна
постоянна и равна  , то математическое ожидание числа появления события
, то математическое ожидание числа появления события 
 суммы очков на двух костях.
суммы очков на двух костях. - количество очков на первой кости
- количество очков на первой кости  - количество очков на второй кости, тогда
- количество очков на второй кости, тогда  , причем
, причем  Составим таблицу:
Составим таблицу:

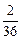










 т.е.
т.е.  .
. , где
, где  .
.
 случайной величины
случайной величины  . Найти параметр
. Найти параметр  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  , функцию распределения случайной величины
, функцию распределения случайной величины  .
.




 , функция
, функция 



 определим функцию распределения случайной величины
определим функцию распределения случайной величины  :
: зная которую, найдем вероятность неравенства
зная которую, найдем вероятность неравенства 





