Основные определения.
1.Гнеденко Б.В. Курс теории вероятности. М.: Высшая школа, 1969г. 2.Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998г. 3. Чистяков В.П. Курс теории вероятностей. М.: Высшая школа, 1982г. 4. Вентцель Е.С., Овчаров Л.А. Теория вероятностей (задачи и упражнения). М.:Высшая школа, 1973г. 5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. М.: Высшая школа, 1998г. 6. Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (типовые расчета). М.: Высшая школа, 1983 г.
Практическое занятие 14-2часа Случайные величины и их числовые характеристики. Дискретные и непрерывные случайные величины. Числовые характеристики. Закон больших чисел. Вопросы: 1. Дайте определение случайной величины. Приведите примеры. 2. Дайте определение функции распределения случайной величины и докажите ее свойства. 3. Дайте определение плотности распределения вероятностей и докажите ее свойства. 4. Дайте описание дискретных и непрерывных распределений: биномиального, пуассоновского, геометрического, гипергеометрического, нормального, показательного, равномерного. 5. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному или показательному закону? 6. Дайте определение многомерной функции распределения случайного вектора и рассмотрите совместные распределения двух случайных величин. 7. Как найти вероятность попадания пары случайных величин в заданный прямоугольник? 8. Сформулируйте теорему о независимых случайных величинах. Что представляет собой распределение суммы независимых случайных величин? 9. Дайте определение математического ожидания случайной величины и докажите его свойства. 10.Дайте определение дисперсии случайной величины и докажите ее свойства. 11. Дайте определение среднего квадратического отклонения случайной величины и укажите его преимущества по сравнению с дисперсией. 12.Сформулируйте теорему Чебышева. 13.Дайте определение характеристическим функциям случайной величины и сформулируйте их свойства. 14.Сформулируйте центральную предельную теорему и теорему Ляпунова. Основные определения. Определение. Случайной называется величина, которая в результате наблюдений может принимать то или иное значение, причем неизвестно какое именно. Будем обозначать случайные величины Функция
называется функцией распределения случайной величины X. Функция распределения обладает следующими свойствами:
Определение. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями, причем число таких значений может быть как конечным так и бесконечным.
|

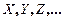 и т.д., а возможные значения соответствующими строчными буквами x, y, z и т.д., например: случайная величина
и т.д., а возможные значения соответствующими строчными буквами x, y, z и т.д., например: случайная величина  имеет три возможных значения х1, х2, х3.
имеет три возможных значения х1, х2, х3. 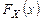 , действительной переменой x,
, действительной переменой x, 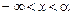 , определяемая формулой
, определяемая формулой ,
,