Однородные дифференциальные уравнения
Определение. Функция Например, функция Функция
Если
где Определение. Дифференциальное уравнение в дифференциальной форме
называется однородным относительно переменных х и у, если
Дифференциальное уравнение в дифференциальной форме
будет однородным в том и только в том случае, когда
легко заключаем, что
Следовательно, уравнение (1) в явном виде всегда можно записать в виде
Пример 1. Проинтегрировать дифференциальное уравнение ►Так как функции Тогда
Предполагая, что х≠0, сокращаем обе части уравнения на
Разделяя переменные, последовательно находим:
В последнее выражение вместо и подставим значение у/х. Получим общий интеграл:
Разрешив его относительно у, найдем общее решение исходного дифференциального уравнения:
Использовав начальное условие у(1)=0, определим значение С:
Следовательно, частное решение исходного уравнения имеет вид
|

 называется однородной функцией измерения
называется однородной функцией измерения  относительно аргументов x и y, если равенство
относительно аргументов x и y, если равенство  справедливо для любого
справедливо для любого  при котором функция
при котором функция  определена,
определена, 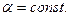
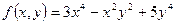 является однородной четвертого измерения
является однородной четвертого измерения  так как
так как 
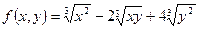 является однородной измерения
является однородной измерения 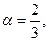 поскольку
поскольку
 поскольку
поскольку 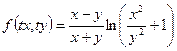 - однородная функция нулевого измерения, так как
- однородная функция нулевого измерения, так как

 (1)
(1) (2)
(2)
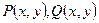 -однородные функции одного и того же измерения
-однородные функции одного и того же измерения 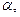 т.е.
т.е.  Действительно, переписав его в нормальной форме:
Действительно, переписав его в нормальной форме:

 то положив
то положив  получим:
получим:
 и найти его частное решение, удовлетворяющее начальному условию у(1)=0.
и найти его частное решение, удовлетворяющее начальному условию у(1)=0. и
и  - однородные второго измерения, то данное уравнение – однородное. Сделаем замену
- однородные второго измерения, то данное уравнение – однородное. Сделаем замену 

 . Далее имеем
. Далее имеем

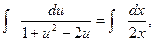



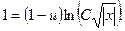 .
.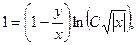
 .
.
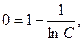
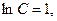
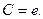
 ◄
◄


