Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения.
Практическое занятие 3 -2 часа Дифференциальные уравнение первого порядка. Уравнение с разделяющимися переменными. Однородные дифференциальные уравнения Основные понятия. Уравнение называется дифференциальным относительно некоторой искомой функции, если оно содержит хотя бы одну производную этой функции. дифференсиального уравнения совпадает(по определению) с порядком наивысшей производной, входящей в это уравнение. Если искомая функция у является функцией одного аргумента х, то дифференциальное уравнение называется обыкновенным. Если же искомая функция зависит от нескольких аргументов, то дифференциальное уравнение называется уравнением в частных производных. Например, уравнение В общем случае дифференциальное уравнение первого порядка может быть записано в виде
Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения. Определение. Уравнение вида
называется дифференциальным уравнением с разделенными переменными. Его общим интегралом будет
где С- произвольная постоянная. Определение. Уравнение вида
или
а также уравнения, которые с помощью алгебраических преобразований приводятся к уравнениям (5) или (6), называются уравнениями с разделяющимися переменными. Разделение переменных в уравнениях (5), (6) выполняется следующим образом. Предположим, что N1(y)≠0, M2(x)≠0, и разделим обе части уравнения (5) на
которые интегрируются, согласно формуле (4):
Пример 1. Найти общее решение дифференциального уравнения
►Предположив, что
Интегрируя его, последовательно находим (произвольную постоянную можно представить в виде
Последнее равенство является общим интегралом уравнение (7). При его нахождении были приняты ограничения Пример 2. Найти частное решение уравнения
удовлетворяющее начальному условию ►Запишем данное уравнение в дифференциальной форме:
Теперь разделим переменные:
Проинтегрируем последнее уравнение:
Получили общее решение исходного уравнения. Использовав начальное условие, определив значение произвольной постоянной:
Следовательно,частное решение исходного уравнения имеет вид
|

 , где
, где  - является обыкновенным дифференциальным уравнением первого порядка, а
- является обыкновенным дифференциальным уравнением первого порядка, а  где
где  - дифференциальным уравнением в частных производных первого порядка.
- дифференциальным уравнением в частных производных первого порядка. (1)
(1) или, если разрешить его относительно
или, если разрешить его относительно  , в явном виде:
, в явном виде:
 . (2)
. (2) (3)
(3)

 (5)
(5)
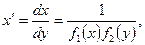 (6)
(6) . Обе части уравнения (1.3) умножим на dx и разделим на f2(y)≠0. В результате получим уравнения с разделенными переменными (т.е. уравнения вида (1.1)):
. Обе части уравнения (1.3) умножим на dx и разделим на f2(y)≠0. В результате получим уравнения с разделенными переменными (т.е. уравнения вида (1.1)):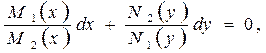



 (7)
(7) и разделив обе части данного уравнения на
и разделив обе части данного уравнения на  получим уравнение с разделенными переменными
получим уравнение с разделенными переменными
 ):
):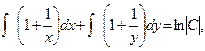



 Однако функции
Однако функции  также является решениями исходного уравнения,что легко проверяется; с другой стороны, они получаются из общего интеграла при С=0. Следовательно,
также является решениями исходного уравнения,что легко проверяется; с другой стороны, они получаются из общего интеграла при С=0. Следовательно,  частные решения уравнения (1).◄
частные решения уравнения (1).◄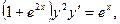
 .
.


 ,
,


 .◄
.◄


