Линейное уравнение
1. Сборник индивидуальных заданий по высшей математике ч.1-3. Под редакцией Рябушко А.П. Минск: Вышейшая школа, 2001г. 2. Высшая математика в упражнениях и задачах. Ч.1,2 Данко П.Е., Попов А.Г., Кожевников Т.Я. М.: Высшая школа,1986 г. 3. Сборник задач по математике для втузов: Линейная алгебра и основы математического анализа. Под редакцией Ефимова А.В., Демидовича Б.П. М.: Наука, 1986г. 4. Кузнецов Л.А.Сборник заданий по высшей математике (типовые расчеты). М.: Высшая школа, 1983 г.
Практическое занятие 4 -2 часа Линейные дифференциальные уравнения. Дифференциальное уравнение Бернулли. Уравнение в полных дифференциалах Линейное уравнение Определение. Уравнение линейное относительно неизвестной функции у и ее производной Функции P(x)≠0, Q(x)≠0 должны быть непрерывными в некоторой области. Общее решение уравнения (2.1) всегда можно записать в виде
где С- произвольная постоянная. Если в уравнении (1) Пример 2. Найти общее решение уравнения ►Приведем данное уравнение к виду (1), разделив обе его части на
Здесь
|

 (1)
(1) (а также любое уравнение, с помощью алгебраических преобразований приводящееся к виду (3)), называется неоднородным линейным дифференциальным уравнением первого порядка.
(а также любое уравнение, с помощью алгебраических преобразований приводящееся к виду (3)), называется неоднородным линейным дифференциальным уравнением первого порядка. (2)
(2)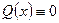 (или
(или  , то получим дифференциальные уравнение с разделяющимися переменными, общее решение которых определяется из уравнения (1) при Q(x)≡0 или Р(х)≡0 соответственно. В случае, когда Q(x)≡0, уравнение (1) называют однородным линейным дифференциальным уравнением.
, то получим дифференциальные уравнение с разделяющимися переменными, общее решение которых определяется из уравнения (1) при Q(x)≡0 или Р(х)≡0 соответственно. В случае, когда Q(x)≡0, уравнение (1) называют однородным линейным дифференциальным уравнением.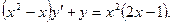 Решить задачу Коши при начальном условии у(-2)=2.
Решить задачу Коши при начальном условии у(-2)=2. Получим:
Получим:





